TANT 21+22 - What's next?

-
Hello there! These are notes for the last two classes of the course "Topics in algebra and number theory" held in Block 4 of the academic year 2017/18 at the University of Copenhagen.

In the latest classes of the course we have struggled with understanding class field theory, which is the study of abelian extensions of a field. More precisely, given a field \( K \) which is either finite, local or global we can define a group \( C_K \) by setting \[ C_K := \begin{cases} \mathbb{Z}, \ \text{if} \ F \ \text{is finite} \\ K^{\times}, \ \text{if} \ F \ \text{is local} \\ \mathbb{I}_K/K^{\times}, \ \text{if} \ F \ \text{is global} \end{cases} \] and class field theory gives us an Artin map \( \theta_K \colon C_K \to G_K^{\text{ab}} \), where \( G_K \) is the absolute Galois group of \( K \). We know moreover that this map has some functoriality property when we change the field \( K \), and that the map \( \widehat{\theta_K} \colon \widehat{C_K} \to G_K^{\text{ab}} \) is an isomorphism. We get in particular that a finite field has only one abelian extension (which is cyclic) of each given degree \( n \) (actually, we know that this is also the only extension of degree \( n \)). Moreover, for a local or global field we get that for every finite abelian extension \( K \subseteq L \) we have that \( \operatorname{Gal}(L/K) \cong C_K/\operatorname{N}_{L/K}(C_L) \).



Problems arising from class field theory

In this section we survey problems that arise immediately after having understood the main statements of class field theory.

Computational class field theory



This description of the Galois groups of finite abelian extensions is already really powerful, but it is not extremely explicit. For number fields (or, more generally, global fields) we obtained a more explicit description by looking at ray class fields and ray class groups. More precisely, we said that for every finite abelian extension \( K \subseteq L \) of a number field \( K \) there exists a modulus \( \mathfrak{m} \) such that \( L \subseteq K(\mathfrak{m}) \) and thus \( \operatorname{Gal}(L/K) \) is a quotient of the ray class group \( \mathfrak{C}_K^{\mathfrak{m}} \). These ray class groups \( \mathfrak{C}_K^{\mathfrak{m}} \) can be computed in a rather explicit way, and there are even algorithms to do so. Thus we have a way to compute every ray class group in a finite time (note that every modulus \( \mathfrak{m} \) is determined by a finite amount of information). Moreover, there exist also algorithms which allow us to compute the ray class field \( K(\mathfrak{m}) \) once we know the group \( \mathfrak{C}_K^{\mathfrak{m}} \). These algorithms are computationally very expensive (exponential in the degree \( [K \colon \mathbb{Q}] \) and in the size of the support of the modulus \( \mathfrak{m} \)) and thus in practice they can be used only in a limited amount of cases. References for this topic include:

Hilbert's twelfth problem


This brings us to another related question: is it possible, given a number field \( K \) to determine all its ray class fields explicitly? More precisely, we would like to have an explicit way to associate to every modulus \( \mathfrak{m} \) an algebraic number \( \alpha_{\mathbb{m}} \in \overline{K} \) such that \( K(\mathfrak{m}) = K(\alpha_{\mathfrak{m}}) \). If \( K = \mathbb{Q} \) we have done this in Example 5 of the previous lecture, where we have seen that \( \alpha_{\mathfrak{m}} = \zeta_{n_{\mathfrak{m}}} \) if \( \mathfrak{m}(\infty) = 1 \) and \( \alpha_{\mathfrak{m}} = \zeta_{n_{\mathfrak{m}}} + \zeta_{n_{\mathfrak{m}}}^{-1} \) if \( \mathfrak{m}(\infty) = 0 \). In particular, every ray class field of \( \mathbb{Q} \) is generated by (linear combinations of) roots of unity, i.e. the values at the integers of the analytic function \( \mathbb{C}^{\times} \to \mathbb{C}^{\times} \) defined by \( z \mapsto e^{2 \pi i/z} \).
In general the problem of determining explicitly the ray class fields of a number field is very difficult, and it is known as Hilbert's 12th problem or Kronecker Jugendtraum (i.e. Kronecker's youth dream). It is for example already really difficult to find an explicit algebraic number \( \alpha_K \in \overline{K} \) such that \( K(\alpha_K) \) is the Hilbert class field of \( K \), i.e. the ray class field corresponding to the trivial modulus. What we know today is how to find explicitly the ray class fields of an imaginary quadratic field \( K = \mathbb{Q}(\sqrt{-n}) \), or more generally of a CM-field, i.e. a totally imaginary field which is a quadratic extension of a totally real one. This is because we can associate to every order in a CM-field an abelian variety (i.e. an algebraic variety which is also an abelian group such that the multiplication and inversion are regular maps) with complex multiplication (that what CM stands for!). One can use the incredibly rich structure of these objects to describe the ray class fields of a CM-field using the torsion part of these abelian groups, and other invariants related to these varieties. References for this topic include:

Class number problems: regular primes


As we have seen in the previous session, finding an explicit description of ray class fields in tough. A first question towards understanding these ray class fields will be to determine explicitly their degrees \( [K(\mathfrak{m}) \colon K] \), i.e. to determine the cardinality of the ray class groups \( \mathfrak{C}_K^{\mathfrak{m}} \). As we have seen in the first section this is doable (in a possibly very long time) if \( K \) and \( \mathfrak{m} \) are given explicitly, but how can we approach this problem in general? For example, can we compute these degrees when we let the number field \( K \) vary in a family?
It turns out that it is already quite hard to compute the class number \( h(K) := \# \mathfrak{C}_K \) of a family of number fields. One instance of this problem dates back to 1850, when Ernst Kummer proved that Fermat's equation \( x^p + y^p = z^p \) does not have any non-trivial solution if \( p \nmid h(\mathbb{Q}(\zeta_p)) \) (see this note by Keith Conrad for an account of the proof). This in particular proves Fermat's last theorem for all the exponents which are products of regular primes, i.e. primes such that \( p \nmid h(\mathbb{Q}(\zeta_p)) \). Unfortunately, this does not prove Fermat's last theorem for every integer because not every prime is regular: for example, Kummer already knew that \( 37 \) is the smallest irregular prime. Today we know that there exist infinitely many irregular primes but we don't know yet if there exist infinitely many regular primes! Siegel conjectured that the density of the regular primes in the set of all primes should be \( 1/\sqrt{e} \sim 60.65 \% \), and this conjecture agrees with computational experiments. References for these topics include:
  • Section 5.3 of the book "Introduction to cyclotomic fields" by Lawrence C. Washington, which contains a proof of the infinitude of irregular primes and an explanation of the heuristic argument of Siegel;
  • the paper "On the counting function of irregular primes" by Florian Luca, Amalia Pizarro-Madariaga and Carl Pomerance for estimates on the number of irregular primes;
  • the paper "Irregular primes to two billion" by William Hart, David Harvey and Wilson Ong for computational evidence of some conjectures regarding regular and irregular primes. 

Class number problems: heuristics 


The questions that we started to face in the previous paragraph can be explored further in many ways. Kummer was dealing with detecting cyclotomic fields \( \mathbb{Q}(\zeta_p) \) whose class group is "small enough" (in particular \( p \nmid h(\mathbb{Q}(\zeta_p) \)). We can push this problem to the extreme by looking at number fields \( K / \mathbb{Q} \) such that \( h(K) = 1 \), i.e. whose ring of integers \( \mathcal{O}_K \) is a unique factorization domain. How many of these fields do we have?

This question is really difficult to deal with: for example it is not know at present if there are infinitely many number fields \( K \) with \( h(K) = 1 \). This is known as the class number one problem and it is widely open in general. Despite this astonishing ignorance, there are some things that we know! For example, we know that if \( d \in \mathbb{N} \) is square-free and \( h(\mathbb{Q}(\sqrt{-d})) = 1 \) then \( d \in \{ 1, 2, 3, 7, 11, 19, 43, 67, 163 \} \). This is a famous result of Stark and Heegner, whose proof uses the description of the ray class fields of imaginary quadratic fields that we outlined in the second session. This is a very beautiful theory, which uses deeply modular forms and elliptic curves to achieve its goals. As you can expect, these results have also been generalized to CM fields, but the generalizations are not as complete or explicit as the result for imaginary quadratic fields.

Finally, one may ask what happens with number fields which are not imaginary quadratic. The simplest answer is that very little is known! Despite this sad news, nowadays we have computational methods to look at the class numbers of families of fields and to try to formulate hypotheses on their behavior. The simplest case in which we can do so is given by the family of real quadratic fields \( \mathbb{Q}(\sqrt{d}) \) for \( d \in \mathbb{N} \) square-free. You can do the experiment by yourself using one of the many free computer packages available for computations in number theory (i.e. PARI-GP or SAGE), or you can look at this sequence on the Online Encyclopedia of Integer Sequences. What you can observe is that there are many, may ones in this sequence, i.e. it seems that a lot of real quadratic fields have class number one... This question attracted the attention of Henry Cohen and Hendrik W. Lenstra Jr., who tried to answer it by means of heuristic arguments.

The key idea of their heuristic is that the probability of appearance of a fixed finite group \( G \) as a class group of some number field should be inversely proportional to \( \#  \operatorname{Aut}(G) \). In particular their conjecture predicts that the density of the set \( \{ d \in \mathbb{N} \mid h(\mathbb{Q}(\sqrt{d}) = 1 \} \) is approximately \( 75.5 \% \), which agrees with what one can observe experimentally!

Is is finally worth to mention that there are a couple of theorems in the direction of understanding the class numbers of families of fields: the theorem of Brauer and Siegel (for general families of fields) and the theorem of Goldfield which relates the class number one problem for imaginary quadratic fields to the conjecture of Birch and Swinnerton-Dyer for elliptic curves with complex multiplication. Using then the deep work of Gross and Zagier which proves this conjecture for a large class of elliptic curves with complex multiplication, one has nowadays a efficient algorithm which in principle would determine the complete list of all imaginary quadratic fields of a given class number.

References for these topics include:

Conductors

As we have seen many times, class field theory for \( \mathbb{Q} \) is simply given by the theorem of Kronecker and Weber, which says that every finite abelian extension of the rationals is contained in a cyclotomic extension. Given such a finite abelian extension \( K / \mathbb{Q} \) we define the conductor of \( K \) as the minimum \( n \in \mathbb{N} \) such that \( K \subseteq \mathbb{Q}(\zeta_n) \). One question arises immediately: how can we compute this conductor? Can we find general formulas for the conductor of families of number fields? The answer to the first question lies in the realm of computational number theory, which was the object of the first section.

Concerning the first question, not a lot is known. As you have seen in the homework, the computation of a formula for the conductor of quadratic fields is related to a famous theorem of Gauß concerning sums of roots of unity (which are now called "Gauß sums"). In particular, the conductor of a quadratic field is always equal to its discriminant.
We have also an explicit formula for the conductor of abelian cubic fields (which are obviously cyclic) which is due to Hasse. There are also formulas for all quartic fields (both cyclic and bi-cyclic) and for quintic fields (which are cyclic). These formulas are explicit in terms of the coefficients of the minimal polynomial of an integral primitive element of the field. A lot of improvement could be made in this area, to obtain even more explicit formulas for the conductor of families of abelian number fields.

References for this part include:

The inverse Galois problem: class field theory and beyond

In the previous sections we dealt with many problems related to class field theory, which is the study of abelian extensions of a number field \( K \). In particular, class field theory tells us that for every abelian extension \( K \subseteq L \) the Galois group \( \operatorname{Gal}(L/K) \) is a quotient of the idelic class group \( C_K \), or (if you prefer) of a ray class group \( \mathfrak{C}_K^{\mathfrak{m}} \) for some modulus \( \mathfrak{m} \). This in particular allows us to decide whether a given (finite) abelian group \( G \) is realizable over \( K \), i.e. if there exists an abelian extension \( K \subseteq L \) with \( \operatorname{Gal}(L/K) \cong G \).

For example we can prove very easily (without using class field theory) that every finite abelian group is realizable over \( \mathbb{Q} \). Suppose first of all that \( G = \mathbb{Z}/n \mathbb{Z} \) is cyclic. Then we can observe that there exists a prime number \( p \in \mathbb{N} \) such that \( p \equiv 1 \, \text{mod} \, n \), as a consequence of Dirichlet's theorem on primes in arithmetic progressions. This implies that \( n \mid p - 1 \), i.e. that there exists a subgroup \( H \) of \( \mathbb{Z}/(p - 1)\mathbb{Z} = (\mathbb{Z}/p \mathbb{Z})^{\times} \) such that \( (\mathbb{Z}/(p - 1)\mathbb{Z})/H \cong \mathbb{Z}/n\mathbb{Z} \). Hence Galois theory implies that there exists a sub-extension \( \mathbb{Q} \subseteq K \subseteq \mathbb{Q}(\zeta_p) \) such that \( \operatorname{Gal}(K/\mathbb{Q}) \cong \mathbb{Z}/n\mathbb{Z} \), i.e. that all cyclic groups are realizable over \( \mathbb{Q} \). To conclude it is sufficient to observe that every finite abelian group \( G \) is a direct product of cyclic groups, say of orders \( n_1,\dots,n_r \) (not necessarily distinct). However we can apply again Dirichlet's theorem on arithmetic progressions to find \( r \) distinct primes \( p_1,\dots,p_r \) such that \( n_j \mid p_j - 1 \) for all \( j \in \{ 1,\dots,r \} \), and this implies that \( G \) can be realized as the Galois group of a sub-extension of \( \mathbb{Q}(\zeta_{p_1\cdots p_r}) \).
The previous theorem was very easy to prove, and tells us that every finite abelian group can be realized as the Galois group of a sub-extension of a cyclotomic field. This must not be confused with the theorem of Kronecker and Weber, which tells us that all the possible finite extensions of \( \mathbb{Q} \) with abelian Galois group arise as sub-extensions of a cyclotomic field.

The immediate question is then: can we prove that some non-abelian groups are realizable? The most important theorem in this direction is a theorem of Igor Shafarevich from 1954, which says that every finite, solvable group is realizable over any global field. This theorem is really deep, and its proof relies heavily on Galois cohomology, i.e. group cohomology applied to Galois groups.
Nowadays we have also many results available for non-solvable groups. We know for example that all the sporadic groups (except possibly Mathieu's group \( M_{23} \) ) are realizable over \( \mathbb{Q} \): among these there is the so called "monster group", which is the largest sporadic simple group, whose order is close to \( 8 \cdot 10^{53} \)! We know moreover that all the projective general linear groups \( \operatorname{PGL}_2(\mathbb{Z}/n \mathbb{Z}) \) are realizable over \( \mathbb{Q} \), and this gives us an infinite family of non-solvable groups which are realizable.

The proofs of all these last results rely on a geometric interpretation of the inverse Galois problem. More specifically, we can ask whether or not a given group \( G \) is realizable not over \( \mathbb{Q} \) but over a different field \( K \), where the question is easier to solve, and then hope to be able to go back and prove the same result over \( \mathbb{Q} \). If we take \( K = \mathbb{C}(t) \) then it is a consequence of Riemann's existence theorem (a classical result in algebraic geometry) that every finite group is realizable over \( K \). Moreover, Hilbert's irreducibility theorem tells us that if a group can be realized over \( \mathbb{Q}(t) \) then it can be realized over \( \mathbb{Q} \). Thus, if we knew how to use that a group \( G \) is realizable over \( \mathbb{C}(t) \) to prove that it is realizable over \( \mathbb{Q}(t) \) we would be done, and this is the content of many if not all the proofs of the realizability of the groups that we have cited in the previous paragraphs.

The inverse Galois problem is thus a natural generalization of class field theory. It aims to study the first, natural question about non-abelian extensions of a number field: do they exist? In more technical words, we are studying the Galois group \( \operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q}^{\text{ab}}) \) which is the part of the absolute Galois group \( G_{\mathbb{Q}} \) that remains after having studied its abelian part \( G_{\mathbb{Q}}^{\text{ab}} \). A conjecture of Shafarevich tells us that the group \( \operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q}^{\text{ab}}) \) should be a free profinite group in infinitely many generators. As a corollary of this result we would have that all the finite groups would be realizable over \( \mathbb{Q} \), which is the main conjecture in the world of inverse Galois problems.

Observe that this wouldn't solve all our questions about inverse Galois theory, but (as usual) will open an incredibly wide area of research! A natural question that we can ask is for example how many extensions of a given number field have Galois group isomorphic to a given group \( G \), and how they "look like". For example we know that we have infinitely many extensions \( L \) of every number field \( K \) with Galois group isomorphic to \( \mathbb{Z}/2 \mathbb{Z} \), and we know that they all have the shape \( L = K(\sqrt{d}) \) for some \( d \in K \) which is not a square. Hence we say that the polynomial \( f(x,t) = x^2 - t \in K[x,t] \) is a generic polynomial for the group \( \mathbb{Z}/2 \mathbb{Z} \), by which we mean that all the extensions of \( K \) with Galois group isomorphic to \( \mathbb{Z}/2 \mathbb{Z} \) are equal to \( K[x]/(f(x,t_0)) \) for some \( t_0 \in K \) which is not a square. In general finding a generic polynomial for a given group might be hard if not impossible! For example, it is impossible to find a generic polynomial for the cyclic groups \( \mathbb{Z}/8 \cdot n \mathbb{Z} \) for all \( n \in \mathbb{N}_{\geq 1} \), as was proved by Hendrik W. Lenstra Jr.
We want finally to say that Gunter Malle conjectured that for every finite, transitive group \( G \) one would have that \[ \# \{ L \supseteq K \mid \operatorname{Gal}(L/K) \cong G, \ \lvert \operatorname{N}_{K/\mathbb{Q}}(\operatorname{disc}(L/K)) \rvert \leq x \} \sim c x^a \log(x)^b \] for some constants \( a,b,c \in \mathbb{R}_{geq 0} \) which can be explicitly computed and depend on \( K \) and \( G \). This conjecture tries to answer the problem of determining the quantity of extensions of a global field with a given Galois group. Unfortunately, this conjecture was proved to be wrong by Klüners, although it is still believed to be true "in most cases". A general conjecture/characterization of the cases in which this conjecture should hold seems to be out of reach.
References for this chapter include:

Beyond class field theory

This section is devoted to questions that arise as generalizations of the main theorems of class field theory. The first and main one is in fact the inverse Galois problem, which is a trait d’union between the world of class field theory and the study of non-abelian extensions of number fields.

Splitting of primes


Let \( K \subseteq L \) be a Galois extension of number fields, and let \( \mathfrak{p} \subseteq \mathcal{O}_K \) be a prime ideal. Then the Galois group \( \operatorname{Gal}(L/K) \) acts transitively on the set of all prime ideals \( \mathfrak{P} \subseteq \mathcal{O}_L \) such that \( \mathfrak{P} \cap \mathcal{O}_K = \mathfrak{p} \). Hence understanding all the possible ways in which a prime of \( \mathcal{O}_K \) splits in \( \mathcal{O}_L \) (i.e. all the possible factorizations of \( \mathfrak{p} \mathcal{O}_L \) as a product of prime ideals) seems to be a first way to understand the extension \( K \subseteq L \). Indeed, this is the only information that we need to determine completely the extension \( K \subseteq L \)! More specifically, a theorem of Michael Bauer tells us that if \( K \subseteq L_1 \) and \( K \subseteq L_2 \) are two Galois extensions then \[ \{ \mathfrak{p} \subseteq \mathcal{O}_K \mid \mathfrak{p} \ \text{splits completely in} \ L_1 \} = \{ \mathfrak{p} \subseteq \mathcal{O}_K \mid \mathfrak{p} \ \text{splits completely in} \ L_2 \}  \] if and only if \( L_1 = L_2 \). Recall that a prime ideal \( \mathfrak{p} \subseteq \mathcal{O}_K \) splits completely in an extension \( K \subseteq L \) if and only if \( \mathfrak{p} \mathcal{O}_L = \mathfrak{P}_1 \cdots \mathfrak{P}_d \), where \( d = [L \colon K] \).
This characterization of finite, Galois extensions in terms of the splitting of prime ideals is a corollary of Chebotarev density theorem, which is a generalization of Dirichlet's unit theorem on arithmetic progressions. More precisely, the theorem says that given a finite, Galois extension of number fields \( K \subseteq L \) then the density of the primes \( \mathfrak{p} \subseteq \mathcal{O}_K \) which are unramified in the extension \( K \subseteq L \) and whose Frobenius conjugacy class \( \operatorname{Frob}_{\mathfrak{p}} \subset \operatorname{Gal}(L/K) \) lies in a particular subset \( X \subseteq \operatorname{Gal}(L/K) \) (which is closed under conjugation) exists and it's equal to \( \# X / \# G \). One interesting fact about this theorem is that it holds for all finite, Galois extensions (abelian or not) but its modern proof reduces the general case to that of abelian extensions, for which class field theory can be used to prove the result very quickly.
References for this section include:

Higher class field theory

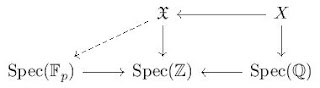
As we have repeated countless times, class field theory is the study of the group \( G_K^{\text{ab}} \) associated to a number field \( K \). Obviously, we can ask this question more generally for every field \( K \), and we already know the answer if \( K \) is a local field or (trivially) if \( K \) is a finite field. For what other kinds of fields could we ask this question?
Well, the first generalization that comes to our mind is to take \( K \) to be a finite extension of \( \mathbb{Q}(t_1,\dots,t_n) \) which is a purely transcendental extension of \( \mathbb{Q} \). Then its finite abelian extensions correspond to function fields of varieties defined over \( K \), and thus geometric methods can be used to try to describe \( G_K^{\text{ab}} \). In particular one can attach to every arithmetic scheme \( X \) (i.e. a generalization of a variety defined over \( \mathbb{Q} \)) a "fundamental group" \( \pi_1(X) \) which generalizes the usual notion of fundamental group of a topological space. More precisely, the fundamental group of a topological space \( T \) can be define as the object which classifies covering maps \( S \to T \). Analogously, the étale fundamental group of a scheme \( X \) can be defined as the group which classifies finite étale coverings \( Y \to X \). Higher class field theory is then the study of the abelian part of this fundamental group (if you want, a sort of "first étale homology group" of \( X \)). This is indeed a generalization of the ordinary class field theory because if \( X = \{ \ast \} \) is the "trivial variety" defined over \( K \) (more precisely, \( X = \operatorname{Spec}(K) \)) then \( \pi_1(X) = G_K \).
References for this section include:

Anabelian geometry and dessin d'enfants

Okay, so we understood that class field theory gives us a way to compute (in some sense) the abelian part of the fundamental group \( \pi_1(X) \) of a variety \( X \) defined over some field (for example, over a number field). But how much information does this fundamental group contain?

This question is the subject of anabelian geometry, a field whose origins go back to the work of Alexander Grothendieck. The original conjecture of Grothendieck in this area was that an hyperbolic curve \( C \) would be completely determined by its fundamental group. This theorem was finally proved by Shinichi Mochizuki. A much simpler result in this area is the theorem of Neukirch and Uchida, which says that an algebraic number field is determined by its absolute Galois group.

Hence, since these fundamental groups carry all this information, in would be really interesting to be able to determine them! One really interesting insight of Alexander Grothendieck was to try to determine (a presentation of) the absolute Galois group \( G_{\mathbb{Q}} \) by looking at its action on objects which are simpler than the algebraic numbers themselves. The dessins d'enfant (child drawings) are objects of this kind which give a combinatorial description of the étale coverings of the space \( \mathbb{P}^1 \setminus {0,1,\infty} \).

As a final remark we want to stress that the ideas of anabelian geometry influenced all the extremely deep susbequent work of Shinichi Mochizuki, which culminated with his claimed proof of the abc conjecture, a much more classical conjecture in Diophantine analysis. 

References for this section include:

Galois representations

So, by now we know how the abelian part of the absolute Galois group \( G_K \) of a number field \( K \) looks like. As we have already discussed, the next step is to study the whole absolute Galois group \( G_{\mathbb{Q}} \) (more generally, \( G_K \) ) or, if you prefer, the "remaining part" \( \operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q}^{\text{ab}}) \), which was conjectured to be a free profinite group by Shafarevich. One approach to study the huge group \( G_{\mathbb{Q}} \) is to study all its possible finite quotients, which would determine the group up to isomorphism because \( G_{\mathbb{Q}} \) is profinite. This is the subject of the inverse Galois problem, that we have already mentioned.

There is also another way to determine the isomorphism class of a group: Tannaka's theorem tells us that a compact topological group (as \( G_{\mathbb{Q}} \) is determined by its linear representations. Thus to study \( G_{\mathbb{Q}} \) it is sufficient to study all the representations \( G_{\mathbb{Q}} \to \operatorname{GL}_n(\kappa) \), where \( \kappa \) is some fixed field. If we take \( \kappa = \mathbb{C} \) and we take a continuous representation \( G_{\mathbb{Q}} \to \operatorname{GL}_n(\mathbb{C}) \) then there exists a finite extension \( \mathbb{Q} \subseteq K \) such that the representation factors through a finite group representation \( \operatorname{Gal}(K/\mathbb{Q}) \to \operatorname{GL}_n(\mathbb{C}) \). This is because \( \operatorname{GL}_n(\mathbb{C}) \) is a (complex) Lie group, and thus has the "no small subgroup" property (indeed, Lie groups are the only locally compact groups with the no-small subgroup property, as Hilbert's fifth problem tells us). These representations are called Artin representations, and constructing them explicitly is really hard.

In order to obtain a richer theory the key observation to make is that there are isomorphisms of fields \( \mathbb{C} \cong \overline{\mathbb{Q}_p} \) for all primes \( p \in \mathbb{N} \). This isomorphism is "very discontinuous", and thus the theory of Artin representations is very different from the theory of continuous representations \( G_{\mathbb{Q}} \to \operatorname{GL}_n(\overline{\mathbb{Q}_p}) \). Nevertheless, one can show that the category of Artin representations is isomorphic to the category of continuous representations \( G_{\mathbb{Q}} \to \operatorname{GL}_n(\overline{\mathbb{Q}_p}) \) with open kernel. Thus, \( p \)-adic representations are far more general, and thus more interesting to study.
Another key reason to study \( p \)-adic representations is that it is "very easy" to define a lot of them explicitly. More specifically, one of the key insights of Grothendieck was to define an "arithmetic cohomology" (i.e. étale cohomology) for varieties defined over the rational numbers, with a natural action of the absolute Galois group. For example if \( A \) is an abelian variety of dimension \( g \) then we can concretely describe the first cohomology group \( H^1_{\text{\'et}}(A_{\overline{\mathbb{Q}}},\overline{\mathbb{Q}_p}) \) as the Tate module of \( A \), which is related to the torsion points of \( A \). Thus \( p \)-adic Galois representations are more natural objects to consider, and we can define a lot of them using étale cohomology. A natural question to ask is: how many of them can be defined in this way? A conjectural answer was given by Fontaine and Mazur, but a full proof to their conjecture is far out of scope.
References for this section include:

L-functions and the Langlands program

So, as we said in the previous section, we would like to understand continuous \( p \)-adic representations \( G_{\mathbb{Q}} \to \operatorname{GL}_n(\mathbb{Q}_p) \). This seems hopeless, because we don't understand the group \( G_{\mathbb{Q}} \) itself, and thus it may be really difficult to understand the matrices that appear in the image of such a representation. Nevertheless, we know that inside \( G_{\mathbb{Q}} \) there are the conjugacy classes \( \operatorname{Frob}_p \) of Frobenius elements lying above the rational primes \( p \in \mathbb{N} \). Hence to every Galois representation \( \rho \colon G_{\mathbb{Q}} \to \operatorname{GL}_n(\mathbb{Q}_p) \) we can associate the sequence of well-defined isomorphism invariants \( (\rho(\operatorname{Frob}_p))_p \). Moreover, these invariants determine \( \rho \) completely if \( \rho \) is semi-simple (which is supposed to be true if \( \rho \) comes from the étale cohomology of an algebraic variety).
Hence since the traces of the Frobenius elements are so important, we could like to put them all together in a unique mathematical object associated to the Galois representation \( \rho \). This object is a Dirichlet series \[ L(\rho,s) = \prod_{p \in \mathcal{P}} \det(\operatorname{Id}_n - p^{-s} \rho(\operatorname{Frob}_p))^{-1} = \sum_{n \in \mathbb{N}} a_n(\rho) \, n^{-s} \] which is a very powerful invariant associated to \( \rho \).

Thus we could try to study a Galois representation \( \rho \) by studying the sequence of coefficients \( (a_n(\rho))_{n \in \mathbb{N}} \). One first simple case in which we may try to do so is when \( \rho \) is obtained by the Tate module of an elliptic curve \( E \) defined over \( \mathbb{Q} \). In this case the modularity theorem of Wiles (et al.) tells us that the Dirichlet series \( \sum_{n \in \mathbb{N}} a_n(\rho) \, e^{(2 \pi i n z)} \) defines... a modular form of weight two! The incredible idea of Robert Langlands was that one could generalize this phenomenon by associating to every Galois representation \( \rho \) an automorphic form, which is a certain "smooth" function on the group \( \operatorname{GL}_n(\mathbb{A}_{\mathbb{Q}}) \) to which we can associate an \( L \)-function which is supposed to coincide with the \( L \)-function of \( \rho \).

References for this section include:

Other topics related to the course

This last section contains some insights about other topics of number theory which are related to what we discussed in the course.

Tate's thesis and generalizations

As we have seen in the course, adèles are a useful tool to define the global Artin map by "gluing together" all the local Artin maps. As Tate writes in the beginning of his PhD dissertation, they were invented by Chevalley to "take analysis out of class field theory". The ring of adèles proved subsequently to be very useful for algebraic number theory in general, because Artin and Whaples showed that global fields are essentially characterized by their ring of adèles and by the product formula.
Thus many people started to wonder if it was possible to to analytic number theory on the ring of adèles. This effort culminated with the PhD thesis of John Tate, in which he developed the theory of Fourier analysis over the ring of adèles \( \mathbb{A}_K \) of a number field \( K \) and used it to give a new and much more elegant proof of the analytic continuation and functional equation of the L-functions associated to Hecke characters, which are continuous group homomorphisms \( C_K \to \mathbb{C}^{\times} \). These characters correspond bijectively (using globla class field theory) to characters of the form \( G_K \to \mathbb{C}^{\times} = \operatorname{GL}_1(\mathbb{C}) \), and the L-functions of these characters are precisely the L-functions of these Galois representations.
This incredible success in the use of abstract Fourier analysis inspired many people to try to do the same thing to prove the analytic continuation and functional equation of more general L-functions. As for now, the success has been limited to the work of Roger Godement and Hervé Jacquet in the 70s, in which they generalized the work of Tate to automorphic forms over more general groups, and the recent work of Ivan Fesenko, which aims to prove the functional equation of the L-function of an elliptic curve by using "higher adelic methods".

References for this section include:

Counting rational points: Weil's conjectures

Let's go back now to the first lecture, when we said that in order to understand \( \mathbb{Z} \) as a ring we need to study the sets of integer solutions of systems of polynomials with integer coefficients. As doing so is really difficult, one possible solution would be to study the solutions of the same system of integral equations modulo a prime \( p \). More specifically, if we suppose that these equations define a scheme of finite type \( X \to \operatorname{Spec}(\mathbb{Z}) \) then we can try to look at the finite sets of points \( X(\mathbb{F}_{p^r}) \). Since these are finite sets, we may say that to study them it's sufficient to determine their cardinality. Thus it makes a lot of sense to study the function \[ \zeta(X_{\mathbb{F}_p}, s) = \exp\left(\sum_{m = 1}^\infty \frac{\# X(\mathbb{F}_{p^m})}{m} p^{-ms}\right) \] which is called the Hasse-Weil zeta function of the variety \( X_{\mathbb{F}_p} \) (the reduction of \( X \) modulo a prime \( p \)). This function was the main protagonist of four deep conjectures of André Weil, which were proved by Bernard Dwork, Alexander Grothendieck and Pierre Deligne. More precisely Bernard Dwork proved that \( \zeta(X_{\mathbb{F}_p}, s) \) is a rational function of \( p^{-s} \), Alexander Grothendieck proved that \( \zeta(X, n - s)=\pm p^{\frac{n E}{2}- E s}\zeta(X,s) \) (where \( n = \dim(X) \) and \( E \) is the Euler characteristic of \( X \)), and Pierre Deligne proved that \( \zeta(X_{\mathbb{F}_p}, s) \) satisfies the Riemann hypothesis, i.e. its zeros lie on a certain "critical line". As a corollary, one gets that the Ramanujan tau function satisfies the bound \( \lvert \tau(p) \rvert \leq 2 \sqrt{p^{11}} \) for all primes \( p \in \mathbb{N} \). These proofs are all incredible pieces of mathematics, and there is hope that the techniques used by Deligne could be used to prove the Riemann hypothesis for the Riemann zeta function \( \zeta(s) \), which is arguably the most important open problem in mathematics.

References for this section include:

Counting rational points: local-global principles and Manin's conjecture

As we said in the previous paragraph, in order to study the ring \( \mathbb{Z} \) we can start to look at solutions of systems of integral equations modulo higher and higher powers of primes. If we want to put all the primes and the powers together, this is equivalent to look at the solutions of these equations in the ring of adèles \( \mathbb{A}_{\mathbb{Q}} \). More precisely, if we have a variety \( X \) defined over \( \mathbb{Q} \) and we want to determine if it has a rational point (i.e. if \( X(\mathbb{Q}) \neq \emptyset \)) then we can try to determine if \( X(\mathbb{A}_{\mathbb{Q}}) \neq \emptyset \) and then try to prove that \( X(\mathbb{Q}) \neq \emptyset \). This can be done for quadrics, as Hasse and Minkowski proved, but unfortunately, Selmer's cubic already provides an example of a variety such that \( X(\mathbb{A}_{\mathbb{Q}}) \neq \emptyset \) but \( X(\mathbb{Q}) = \emptyset \). Thus people tried to investigate what "obstructs" the Hasse principle, i.e. what makes \( X(\mathbb{Q}) = \emptyset \) even if \( X(\mathbb{A}_{\mathbb{Q}}) \neq \emptyset \). A first answer is given by the Brauer-Manin obstruction, i.e. the fact that \( X(\mathbb{Q}) \) lies in a certain subspace \( X(\mathbb{A}_{\mathbb{Q}})^{\text{Br}} \) of \( X(\mathbb{A}_{\mathbb{Q}}) \) defined as the left kernel of a pairing \( X(\mathbb{A}_{\mathbb{Q}}) \times \operatorname{Br}(X) \to \mathbb{Q}/\mathbb{Z} \). Here \( \operatorname{Br}(X) := H^2_{\text{ét}}(X,\mathbb{G}_m) \) is the Brauer group of the scheme \( X \), an important invariant which can also be used to detect the rationality of the variety \( X \). Unfortunately, it has been shown now that this is not the only obstruction for the Hasse principle to hold, i.e. there are varieties with \( X(\mathbb{A}_{\mathbb{Q}})^{\text{Br}} \neq \emptyset \) but with \( X(\mathbb{Q}) = \emptyset \). It is an open problem to determine an exaustive list of obstructions to the Hasse principle, and to characterize the varieties \( X \) for which the Brauer-Manin obstruction is the only obstruction to the Hasse principle.

Finally, one may ask: if \( X(\mathbb{Q}) \neq \emptyset \), how many rational points do we have? This is a very difficult question: for example, if \( X \) is a curve of genus bigger or equal to \( 2 \) then Louis Joel Mordell conjectured that \( X(\mathbb{Q}) \) is a finite set. This conjecture was proved by Gerd Faltings and (later on) by Paul A. Vojta and Enrico Bombieri, and its proof uses deep techniques from the theory of abelian varieties and from Diophantine geometry. In general, there is a conjecture of Manin which predicts how many rational points of bounded height we should have on a variety: many special cases of this conjecture are known, but it remains widely open in general.

References for this section include:

Comments

Post a Comment

Popular posts from this blog

A (not quite) perfect(oid) talk

-
Image
Hi all! These are notes for a talk that I gave at a seminar on the work of Bhargav Bhatt , Matthew Morrow and Peter Scholze ( I and II ) organized in Copenhagen by Elden Elmanto . The aim of this talk was to introduce the main results of the two papers, and the categories \( \mathbf{QSyn} \) and \( \mathbf{QRSPerfd} \) that appear in the second paper. As the discussions went on for a long time, I managed only to achieve this second task, but I will post here the original notes for the talk, which might be used for a follow-up talk later on. Disclaimer : these notes have not been fully revised and most likely contain a wide variety of errors, misprints and imprecisions. Please use them at your own risk! Moreover, your comments are more than welcome! Introduction The first goal of the papers of Bhatt-Morrow-Scholze is to define two cohomology theories which can be used to recover étale , crystalline and de Rham cohomology . This is very interesting from the point of view of
Read more

TANT 1 - An introduction to p-adic numbers (and much more)

-
Hello everyone! These are notes for the first class of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . This will be a course on p-adic numbers, so in this first hour I tried to give a little motivation about why one should study these objects in relation to some fundamental questions in number theory.
Read more

TANT 19 - Global class field theory

-
Image
Hello there! These are notes for the nineteenth class of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . In the last lecture we defined the ring of adèles \( \mathbb{A}_K \), the group of idèles \( \mathbb{I}_K := \mathbb{A}_K^{\times} \) and the idèle class group \( C_K := \mathbb{I}_K/K^{\times} \) of a global field \( K \). We have moreover seen that we can construct a continuous group homomorphism \( \mathbb{I}_K \to G_K^{\text{ab}} \) by gluing together all the local Artin maps. The biggest deal to complete the proof of the main theorem of global class field theory is then to show that this map is surjective and its kernel contains \( K^{\times} \). Thus, this map induces a global Artin map \( \theta_K \colon C_K \to  G_K^{\text{ab}} \) which in turn induces an isomorphism \( \widehat{C_K} \cong G_K^{\text{ab}} \). This isomorphism will give us a bijective correspondence between open
Read more