A (not quite) perfect(oid) talk
Hi all! These are notes for a talk that I gave at a seminar on the work of Bhargav Bhatt, Matthew Morrow and Peter Scholze (I and II) organized in Copenhagen by Elden Elmanto.
The aim of this talk was to introduce the main results of the two papers, and the categories \( \mathbf{QSyn} \) and \( \mathbf{QRSPerfd} \) that appear in the second paper. As the discussions went on for a long time, I managed only to achieve this second task, but I will post here the original notes for the talk, which might be used for a follow-up talk later on.
Disclaimer: these notes have not been fully revised and most likely contain a wide variety of errors, misprints and imprecisions. Please use them at your own risk! Moreover, your comments are more than welcome!
More precisely, if we want to study the object \( \mathbb{Z} \in \mathbf{CRing} \) we may as well (by means of the Yoneda lemma) study all the possible maps \( R \to \mathbb{Z} \), and since \( \mathbb{Z} \) is initial in \( \mathbf{CRing} \) we know that \( R \cong \mathbb{Z}[\{x_j\}_{j \in J}]/(\{f_i\}_{i \in I}) \) for a (possibly infinite) number of variables and a possibly infinite number of equations, each one in a finite number of variables. Hence studying \( \mathbb{Z} \) is equivalent to studying Diophantine equations, i.e. the sets of integer solutions of polynomial equations with integer coefficients.
Studying these kind of equations is notoriously a difficult problem, as it's shown for instance by the complexity of the proofs of Fermat's last theorem and Catalan's conjecture. Hence it seems impossible to look for a general method to solve these equations. Nevertheless, in a wide variety of situations we can gain more insight by looking for algebraic solutions to our equation of interest and let the absolute Galois group act on this set.
More precisely, if \( f \in \mathbb{Z}[x_1,\dots,x_n] \) we define \( \mathcal{P}_f := \operatorname{Proj}(\mathbb{Z}[x_0,\dots,x_n]/ {^h\!f}) \), where \( ^h\!f \in \mathbb{Z}[x_0,x_1,\dots,x_n] \) is the homogenization of \( f \). Then \( \mathcal{P}_f(\mathbb{Z}) \) is (closely related to) the set of solutions of the Diophantine equation \( f = 0 \), and we have that \( \mathcal{P}_f(\mathbb{Z}) = \mathcal{P}_f(\mathbb{Q}) = \mathcal{P}_f(\overline{\mathbb{Q}})^{G_{\mathbb{Q}}} \) where \( G_{\mathbb{Q}} = \operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q}) \). Thus to study the set \( \mathcal{P}_f(\mathbb{Z}) \) we can study the action of \( G_{\mathbb{Q}} \) on \( \mathcal{P}_f(\overline{\mathbb{Q}}) \).
If \( f \in \mathbb{Z}[x] \) we can use the fact that \( \mathcal{P}_f(\overline{\mathbb{Q}}) = \mathcal{P}_f(\mathbb{C}) \subseteq \mathbb{CP}^1 \) is a finite discrete set (when endowed with the subspace topology) and that the action of \( G_{\mathbb{Q}} \) is (obviously) continuous to get an action of \( G_{\mathbb{Q}} \) on the singular cohomology \( \operatorname{GL}(H^0_{\text{sing}}(\mathcal{P}_f(\mathbb{C}),\mathbb{C})) \). For polynomials in more than one variable we can't do this anymore because \( \mathcal{P}_f(\overline{\mathbb{Q}}) \neq \mathcal{P}_f(\mathbb{C}) \) and also because the action of \( \operatorname{Aut}_{\mathbb{Q}}(\mathbb{C}) \) on \( \mathcal{P}_f(\mathbb{C}) \) is wildly discontinuous (if we consider \( \mathcal{P}_f(\mathbb{C}) \subset \mathbb{CP}^n \) with the subspace topology), and thus does not induce an action on singular cohomology.
To overcome this difficulty the French school of algebraic geometry (and in particular of Alexander Grothendieck) that one can define a new cohomology theory \( H^{\ast}_{\text{ét}}((\mathcal{P}_f)_{\overline{\mathbb{Q}}},\mathbb{Q}_p) \) on which \( G_{\mathbb{Q}} \) acts continuously, and which allows us to recover singular cohomology by means of the comparison isomorphism \( H^{\ast}_{\text{ét}}((\mathcal{P}_f)_{\overline{\mathbb{Q}}},\mathbb{Q}_p) \cong H^{\ast}_{\text{sing}}(\mathcal{P}_f(\mathbb{C}),\mathbb{Z}) \otimes_{\mathbb{Z}} \mathbb{Q}_p \) (if \( \mathcal{P}_f \) is smooth). Hence for every \( f \in \mathbb{Z}[x_1,\dots,x_r] \) and every \( i \in \{ 0,\dots,2 r\} \) we have representations \( G_{\mathbb{Q}} \to \operatorname{GL}_{n_i}(\mathbb{Q}_p) \), where \( n_i = \dim_{\mathbb{Q}_p}(H^{i}_{\text{ét}}((\mathcal{P}_f)_{\overline{\mathbb{Q}}},\mathbb{Q}_p)) \). Observe now that for every prime \( l \in \mathbb{N} \) we have that \( G_{\mathbb{Q}_l} \subseteq G_{\mathbb{Q}} \), and for all but a finite number of primes the induced representation \( G_{\mathbb{Q}_l} \to \operatorname{GL}_{n_i}(\mathbb{Q}_p) \) is unramified, i.e. it is trivial on the inertia subgroup \( I_{\mathbb{Q}_l} := \ker(G_{\mathbb{Q}_l} \twoheadrightarrow G_{\mathbb{F}_l}) \). This never happens for \( l = p \), which is one of the reasons to consider another cohomology theory (called crystalline cohomology), which is analogous to de Rham cohomology and is more suited for this situation. This rises the question of finding an analogue to de Rham's theorem in this context, which was proved by Gerd Faltings (see here) and can now be seen as a consequence of the work of Bhatt-Morrow-Scholze. We will get back to this.
To motivate the study of perfectoid rings and perfectoid spaces we can go back to Galois representations. More precisely, if \( \rho \colon G_{\mathbb{Q}} \to \operatorname{GL}_n(\mathbb{Q}_p) \) is a continuous group homomorphism which is unramified at finitely many places (i.e. \( I_{\mathbb{Q}_l} \subseteq \ker(\rho) \) for all but finitely many primes \( l \in \mathbb{N} \) ) then Chebotarev's density theorem tells us that \( \rho \) is determined (up to semi-semplification) by the characteristic polynomials of \( \rho([\operatorname{Frob}_l]) \), where \( [\operatorname{Frob}_l] \) is the conjugacy class of Frobenius elements associated to primes lying above the prime \( l \in \mathbb{N} \). These polynomials can be "assembled together" to define the L-function \( L(\rho,s) \) associated to \( \rho \) which determines \( \rho \) up to semi-semplification (see these notes by Takeshi Saito). These functions are the central object of the Langlands program, which aims to relate them to L-functions of a more analytic nature (associated to automorphic forms). Moreover studying their zeros is an incredibly complicated problem, which is (most likely) still open even for the simplest L-function, the Riemann zeta function \( \zeta(s) \) which is associated to the trivial representation of \( G_{\mathbb{Q}} \).
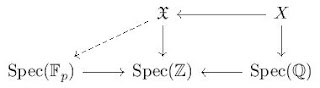This problem is known to hold for Galois representations which come from varieties over finite fields, as was proved by Pierre Deligne. More precisely if \( \mathfrak{X} \to \operatorname{Spec}(\mathbb{Z}) \) is a scheme of finite type whose structural morphism factors through \( \operatorname{Spec}(\mathbb{F}_p) \) for some prime \( p \in \mathbb{N} \) then the L-function of the Galois representation given by the action of \( G_{\mathbb{Q}} \) on \( H^i_{\text{ét}}(X_{\overline{\mathbb{Q}}},\mathbb{Q}_l) \) (for \( l \neq p \) ) satisfies the Riemann hypothesis, where \( X = \mathfrak{X}_{\mathbb{Q}} \) is the generic fiber of \( \mathfrak{X} \). Thus it might be nice to have a theory which helps us to compare varieties in characteristic zero to varieties in positive characteristic, and this is precisely one of the aims of the theory of perfectoid spaces.
In particular, this theory starts with the definition of a perfectoid field, and then defines a perfectoid algebra and a perfectoid space over such a field. We will instead introduce perfectoid rings directly, as it is done in Section 3 of the first paper of Bhatt, Morrow and Scholze. To do so we need to talk about perfect rings, perfections and the period ring \( \mathbb{A}_{\text{inf}} \) defined by Fontaine.
Let \( p \in \mathbb{N} \) be a prime number (which will be fixed in what follows) and \( R \) a ring of characteristic \( p \). Then \( R \) is said to be perfect if the Frobenius map \( R \to R \) defined by \( x \mapsto x^p \) is an isomorphism. Recall in particular that the Frobenius is always a ring map because in positive characteristic we have the freshmen's dream identity \( (x+y)^p = x^p + y^p \).
Let now \( \iota \colon \mathbf{Perf}_{\mathbb{F}_p} \hookrightarrow \mathbf{Alg}_{\mathbb{F}_p} \) denote the full sub-category of perfect rings in characteristic \( p \). Then we have two functors \( (-)^{\text{perf}}, (-)_{\text{perf}} \colon \mathbf{Alg}_{\mathbb{F}_p} \to \mathbf{Perf}_{\mathbb{F}_p} \) which are related to \( \iota \) by the adjunctions \( (-)_{\text{perf}} \dashv \iota \dashv (-)^{\text{perf}} \), and can be defined as \( R^{\text{perf}} := \varprojlim_{\varphi} R \) and \( R_{\text{perf}} := \varinjlim_{\varphi} R \), where \( \varphi \colon R \to R \) is the Frobenius map.
We have finally a tilt functor \( (-)^{\flat} \colon \mathbf{CRing} \to \mathbf{Perf}_{\mathbb{F}_p} \) defined as \( R^{\flat} := (R/p R)^{\text{perf}} \) and it is not difficult to show that \( R^{\flat} \cong \varprojlim_{x \mapsto x^p} R \) as multiplicative monoids (see Lemma 2.0.6 of these notes of Bhargav Bhatt). This identification gives us a multiplicative map \( (-)^{\sharp} \colon R^{\flat} \to R \) by projecting onto the first component of the projective limit. This map clearly becomes a ring homomorphism if we compose it with the quotient map \( R \twoheadrightarrow R/p R \).
Now we can define the functor \( \mathbb{A}_{\text{inf}} \colon \mathbf{CRing} \to \mathbf{CRing} \) as \( \mathbb{A}_{\text{inf}}(R) := W(R^{\flat}) \), where \( W \colon \mathbf{Perf}_{\mathbb{F}_p} \to \mathbf{CRing} \) is the functor which associates to a perfect ring \( R \) of characteristic \( p \) its ring of Witt vectors \( W(R) \).
The construction of Witt vectors can be made very explicit (see these notes of Joseph Rabinoff), but for us it will be sufficient to recall that \( W(R) \) is (up to isomorphism) the unique \( p \)-adically complete ring such that \( p \) is not a zero divisor in \( W(R) \) and \( W(R)/p W(R) \cong R \). Moreover one can show that the quotient map \( W(R) \twoheadrightarrow R \) admits a unique multiplicative section \( [-] \colon R \to W(R) \) which is called the Teichmüller map, and every element \( x \in W(R) \) admits a unique expansion \( x = \sum_{n = 0}^{+\infty} \ [x_n] \, p^n \).
Using this one can prove the universal property of Witt vectors, i.e. the fact that for every \( p \)-adically complete ring \( S \) the map \( \operatorname{Hom}(W(R),S) \to \operatorname{Hom}(R,S/p S) \) obtained by reducing modulo \( p \) is a bijection (see Theorem 6.6 of Rabinoff's notes).
This finally gives us a map \( \Theta \colon \mathbb{A}_{\text{inf}}(R) \to R \) for every \( p \)-adically complete ring \( R \), which is induced by the ring homomorphism \( (-)^{\sharp} \colon R^{\flat} \to R/p R \).
We are now able to define a perfectoid ring as in Definition 3.5 of the first paper of Bhatt, Morrow and Scholze. More precisely, a ring \( R \) is said to be perfectoid (at the prime \( p \)) if it is semi-perfect (i.e. the Frobenius map \( R/p \to R/p \) is surjective), it is \( \pi \)-adically complete for some \( \pi \in R \) with \( \pi^p \mid p \) (which implies that \( R \) is \( p \)-adically complete) and if the kernel of \( \Theta \colon \mathbb{A}_{\text{inf}}(R) \to R \) is principal. We will denote by \( \mathbf{Perfd_p} \hookrightarrow \mathbf{CRing} \) the full subcategory of rings which are perfectoid at the prime \( p \).
We can now state the main results of Section 6.1 of the second paper of Bhatt, Morrow and Scholze, which computes these functors on perfectoid rings. More precisely, for every perfectoid ring \( R \in \mathbf{Perfd_p} \) we have that \[ \pi_{\ast}(\operatorname{THH}(R)^{\wedge p}) = \mathbb{A}_{\text{inf}}(R)[u] \qquad \pi_{\ast}(\operatorname{TP}(R)^{\wedge p}) = \mathbb{A}_{\text{inf}}(R)[\sigma,\sigma^{-1}] \qquad \pi_{\ast}(\operatorname{TC}^{-}(R)^{\wedge p}) \cong \frac{\mathbb{A}_{\text{inf}}(R)[X,Y]}{(X Y - \xi)} \] where \( u \in \pi_2(\operatorname{THH}(R)^{\wedge p}) \cong \ker(\Theta)/\ker(\Theta)^2 \), \( \sigma \in \pi_2(TP(R)^{\wedge p}) \) and \( \xi \in \ker(\Theta) \) are generators.
These identifications allow us to describe the functors \( \pi_{\ast}(\operatorname{THH}(-)^{\wedge p}), \pi_{\ast}(\operatorname{TP}(-)^{\wedge p}), \pi_{\ast}(\operatorname{TC}^{-}(-)^{\wedge p}) \) on the bigger category \( \mathbf{QSyn}_p \hookrightarrow \mathbf{CRings} \) of quasi-syntomic rings, because they are sheaves for a suitable Grothendieck topology which has the property that every sheaf is determined by its values on the smaller category \( \mathbf{QRSPerfd}_p \hookrightarrow \mathbf{QSyn}_p \) which is closely related to \( \mathbf{Perfd}_p \hookrightarrow \mathbf{QRSPerfd}_p \) (see Proposition 4.30 of the second paper of Bhatt, Morrow and Scholze).
This fits into a general pattern in derived algebraic geometry, when to understand a certain functor \( F \colon \mathcal{C} \to \mathcal{D} \) we restrict it to a suitably small sub-category \( \mathcal{C}_0 \hookrightarrow \mathcal{C} \) on which we know how this functor behaves, we extend this restriction formally to a bigger category \( \widetilde{\mathcal{C}_0} \) and we find a functor \( \mathcal{C} \hookrightarrow \widetilde{\mathcal{C}_0} \) which makes the diagram on the right commutative and gives us a better understanding of the functor \( F \).
Moreover recall that if \( R \) is a ring and \( C_{\bullet} \in \operatorname{D}(R) \) is a complex of \(R\)-modules we say that \( C_{\bullet} \) has \( p \)-complete Tor amplitude in \( [a,b] \) (for some integers \( a \leq b \) ) if for every \( R/p R \)-module \( M \) the complex \( (C_{\bullet} \otimes_R^{\mathbb{L}} R/p R) \otimes_{R/p R}^{\mathbb{L}} M \) is concentrated in degrees \( a, a+1, \dots, b \).
Using the cotangent complex we can now define a map of rings \( A \to B \) to be quasi-syntomic (at a prime \( p \in \mathbb{N} \) ) if \( A^{\wedge p} \to B^{\wedge p} \) is flat and \( L_{B/A} \) has p-complete Tor amplitude in \( [-1,0] \). The reason for this name is that if \( A \to B \) is quasi-syntomic, \( A \) and \( B \) are Noetherian and \( B \) is of finite type over \( A \) then the map \( A^{\wedge p} \to B^{\wedge p} \) is syntomic, i.e. it's flat, of finite presentation and a local complete intersection.
Moreover we say that a quasi-syntomic map \( A \to B \) is a quasi-syntomic cover if \( A^{\wedge p} \to B^{\wedge p} \) is faithfully flat.
Now a ring \( R \) is said to be quasi-syntomic (at a prime \( p \)) if it is \( p \)-complete, if it has bounded \( p \)-torsion and if \( L_{A/\mathbb{Z}_p} \) has \( p \)-complete Tor amplitude in \( [-1,0] \). We denote by \( \mathbf{QSyn}_p \hookrightarrow \mathbf{CRing} \) the full subcategory of quasi-syntomic rings, and we endow it with the Grothendieck topology whose covering families are quasi-syntomic covers.
Moreover the category \( \mathbf{QRSPerfd}_p \) of quasi-regular, semi-perfectoid rings (at the prime \( p \) ) is the full sub-category of \( \mathbf{QSyn}_p \) whose objects are all the quasi-syntomic rings \( S \) which are semi-perfect and admit a map \( R \to S \) with \( R \in \mathbf{Perfd}_p \).
Observe now that \( \mathbf{Perfd}_p \hookrightarrow \mathbf{QRSPerfd}_p \) because if \( R \) is a perfectoid ring (at the prime \( p \in \mathbb{N} \) then \( R[p^{\infty}] = R[p] \) and \( L_{R/\mathbb{Z}_p} \) has \( p \)-complete Tor amplitude in \( [-1,-1] \). This last observation can be proved by looking at the triangle \( L_{\mathbb{A}_{\text{inf}}(R)/\mathbb{Z}_p} \otimes^{\mathbb{L}}_{\Theta} R \to L_{R/\mathbb{Z}_p} \to L_{R/\mathbb{A}_{\text{inf}}(R)} \) where the first element becomes trivial after \( p \)-completion and \( L_{R/\mathbb{A}_{\text{inf}}(R)} \cong \ker(\Theta)/\ker(\Theta)^2[1] \) because \( \ker(\Theta) \) is generated by a non-zero divisor (see Lemma 3.10 of the first paper of Bhatt, Morrow and Scholze).
As we said, the category \( \mathbf{QRSPerfd}_p \) is defined because one can extend the computations of \( \operatorname{THH} \), \( \operatorname(TP) \) and \( \operatorname{TC}^{-} \) from \( \mathbf{Perfd}_p \) to \( \mathbf{QRSPerfd}_p \), as it is explained in Section 7 of the second paper of Bhatt, Morrow and Scholze.
In the original paper, Scholze defines a perfectoid field (at a prime \( p \in \mathbb{N} \) ) as a complete, non-Archimedean field \( K \) with residue characteristic \( p > 0 \) such that \( \lvert K^{\times} \rvert \) is not discrete and \( \mathcal{O}_K := \{ x \in K \colon \lvert x \rvert \leq 1 \} \) is semi-perfect. One can show that this happens if and only if \( \mathcal{O}_K \) is perfectoid in our sense.
More generally, there is a comparison between the notion of a perfectoid Tate ring in the sense of Fontaine and the notion of perfectoid ring in the sense of Bhatt, Morrow and Scholze. Recall that a ring \( R \) is a Tate ring if and only if it is a topological ring for which there exists a sub-ring \( R_0 \subseteq R \) on which the topology is \( \pi \)-adic for some element \( \pi \in R_0 \) for which \( R = R_0[1/\pi] \). In this situation we can say that a subset \( S \subseteq R \) is bounded if \( S \subseteq t^{-n} A_0 \) for some \( n \in \mathbb{N} \), and we can define the subring \( R^{\circ} \subseteq R \) of elements whose set of powers is bounded. With these notions we define a Tate ring \( R \) to be perfectoid (in the sense of Fontaine) if \( R^{\circ} \) is bounded and there is \( \pi \in R \) which is topologically nilpotent such that \( \pi^p \mid p \) and the Frobenius map on \( R^{\circ}/ \pi^p R^{\circ} \) is surjective. Then one can show that if \( R \) is a Tate ring which is perfectoid in Fontaine's sense then every open and integrally closed subring \( R^{\dagger} \subseteq R^{\circ} \) is perfectoid. Moreover, if a Tate ring \( R \) contains a perfectoid bounded sub-ring \( R^{\dagger} \subseteq R^{\circ} \) which is open and integrally closed then \( R \) is perfectoid in Fontaine's sense. Finally, for every perfectoid ring \( R \) which is \( \pi \)-adically complete for some \( \pi \in R \) with \( \pi \mid p \) we have that \( R[1/\pi] \) is a Tate ring and is perfectoid in Fontaine's sense. For the proof of these results see Lemma 3.20 and 3.21 of the first paper of Bhatt, Morrow and Scholze.
Finally, we recall how one can define adic and perfectoid spaces starting from Tate rings. More precisely if \( A \) is a Tate ring and \( A^{\dagger} \subseteq A^{\circ} \) is an open and integrally closed subring we define \( \operatorname{Spa}(A,A^{\dagger}) \) to be the set of all absolute values \( \lvert \cdot \rvert \colon A \to \Gamma \cup \{ 0 \} \) (where \( \Gamma \) is a totally ordered multiplicative abelian group) such that \( \lvert x \rvert \leq 1 \) for all \( x \in A^{\dagger} \) and \( \lvert \cdot \rvert \) is continuous with respect to the order topology on the target, quotiented out by the equivalence relation given by \( \lvert \cdot \rvert_1 \sim \lvert \cdot \rvert_2 \) when \( \lvert x \rvert_1 \geq \lvert y \rvert_1 \) if and only if \( \lvert x \rvert_2 \geq \lvert y \rvert_2 \). This set is given the topology generated by the subsets of the form \( \{ \lvert \cdot \rvert \in \operatorname{Spa}(A,A^{\dagger}) \colon \lvert f \rvert \leq \lvert g \rvert \} \) for \( f, g \in A \).
This topological space is called affinoid, and it's moreover called affinoid perfectoid if \( A \) is perfectoid in Fontaine's sense, or if \( A^{\dagger} \) is perfectoid in the sense of Bhatt, Morrow and Scholze.
An adic space is then defined by glueing these topological spaces, and a perfectoid space is defined by glueing affinoid perfectoids. For the problems given by this glueing (for example, the definition of a sheaf on \( \operatorname{Spa}(A,A^{\dagger}) \) ) see Lecture II and III of these notes by Jared Weinstein and Peter Scholze).
Three of the most surprising applications of the theory of perfectoid spaces are:
As we have already said, the original plan was to cover also the main properties of the two cohomology theories defined in Bhatt, Morrow and Scholze (one over \( \mathbb{A}_{\text{inf}}(\mathcal{O}_C) \) for a complete, algebraically closed non-Archimedean field \( C \) and the other on \( \mathfrak{S}(\mathcal{O}_K) := W(\mathcal{O}_K/\mathfrak{m}_K)\llbracket z \rrbracket \) for a \( p \)-adic field \( K \) ) and to see how one can "visualize" the ring \( \mathbb{A}_{\text{inf}}(R) \) by means of the curve of Fargues and Fontaine. We will hopefully keep these topics for a subsequent talk!
The aim of this talk was to introduce the main results of the two papers, and the categories \( \mathbf{QSyn} \) and \( \mathbf{QRSPerfd} \) that appear in the second paper. As the discussions went on for a long time, I managed only to achieve this second task, but I will post here the original notes for the talk, which might be used for a follow-up talk later on.
Disclaimer: these notes have not been fully revised and most likely contain a wide variety of errors, misprints and imprecisions. Please use them at your own risk! Moreover, your comments are more than welcome!
Introduction
The first goal of the papers of Bhatt-Morrow-Scholze is to define two cohomology theories which can be used to recover étale, crystalline and de Rham cohomology. This is very interesting from the point of view of arithmetic, because it gives us a new tool that we can use to study the integers as a ring.More precisely, if we want to study the object \( \mathbb{Z} \in \mathbf{CRing} \) we may as well (by means of the Yoneda lemma) study all the possible maps \( R \to \mathbb{Z} \), and since \( \mathbb{Z} \) is initial in \( \mathbf{CRing} \) we know that \( R \cong \mathbb{Z}[\{x_j\}_{j \in J}]/(\{f_i\}_{i \in I}) \) for a (possibly infinite) number of variables and a possibly infinite number of equations, each one in a finite number of variables. Hence studying \( \mathbb{Z} \) is equivalent to studying Diophantine equations, i.e. the sets of integer solutions of polynomial equations with integer coefficients.
Studying these kind of equations is notoriously a difficult problem, as it's shown for instance by the complexity of the proofs of Fermat's last theorem and Catalan's conjecture. Hence it seems impossible to look for a general method to solve these equations. Nevertheless, in a wide variety of situations we can gain more insight by looking for algebraic solutions to our equation of interest and let the absolute Galois group act on this set.
More precisely, if \( f \in \mathbb{Z}[x_1,\dots,x_n] \) we define \( \mathcal{P}_f := \operatorname{Proj}(\mathbb{Z}[x_0,\dots,x_n]/ {^h\!f}) \), where \( ^h\!f \in \mathbb{Z}[x_0,x_1,\dots,x_n] \) is the homogenization of \( f \). Then \( \mathcal{P}_f(\mathbb{Z}) \) is (closely related to) the set of solutions of the Diophantine equation \( f = 0 \), and we have that \( \mathcal{P}_f(\mathbb{Z}) = \mathcal{P}_f(\mathbb{Q}) = \mathcal{P}_f(\overline{\mathbb{Q}})^{G_{\mathbb{Q}}} \) where \( G_{\mathbb{Q}} = \operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q}) \). Thus to study the set \( \mathcal{P}_f(\mathbb{Z}) \) we can study the action of \( G_{\mathbb{Q}} \) on \( \mathcal{P}_f(\overline{\mathbb{Q}}) \).
If \( f \in \mathbb{Z}[x] \) we can use the fact that \( \mathcal{P}_f(\overline{\mathbb{Q}}) = \mathcal{P}_f(\mathbb{C}) \subseteq \mathbb{CP}^1 \) is a finite discrete set (when endowed with the subspace topology) and that the action of \( G_{\mathbb{Q}} \) is (obviously) continuous to get an action of \( G_{\mathbb{Q}} \) on the singular cohomology \( \operatorname{GL}(H^0_{\text{sing}}(\mathcal{P}_f(\mathbb{C}),\mathbb{C})) \). For polynomials in more than one variable we can't do this anymore because \( \mathcal{P}_f(\overline{\mathbb{Q}}) \neq \mathcal{P}_f(\mathbb{C}) \) and also because the action of \( \operatorname{Aut}_{\mathbb{Q}}(\mathbb{C}) \) on \( \mathcal{P}_f(\mathbb{C}) \) is wildly discontinuous (if we consider \( \mathcal{P}_f(\mathbb{C}) \subset \mathbb{CP}^n \) with the subspace topology), and thus does not induce an action on singular cohomology.
To overcome this difficulty the French school of algebraic geometry (and in particular of Alexander Grothendieck) that one can define a new cohomology theory \( H^{\ast}_{\text{ét}}((\mathcal{P}_f)_{\overline{\mathbb{Q}}},\mathbb{Q}_p) \) on which \( G_{\mathbb{Q}} \) acts continuously, and which allows us to recover singular cohomology by means of the comparison isomorphism \( H^{\ast}_{\text{ét}}((\mathcal{P}_f)_{\overline{\mathbb{Q}}},\mathbb{Q}_p) \cong H^{\ast}_{\text{sing}}(\mathcal{P}_f(\mathbb{C}),\mathbb{Z}) \otimes_{\mathbb{Z}} \mathbb{Q}_p \) (if \( \mathcal{P}_f \) is smooth). Hence for every \( f \in \mathbb{Z}[x_1,\dots,x_r] \) and every \( i \in \{ 0,\dots,2 r\} \) we have representations \( G_{\mathbb{Q}} \to \operatorname{GL}_{n_i}(\mathbb{Q}_p) \), where \( n_i = \dim_{\mathbb{Q}_p}(H^{i}_{\text{ét}}((\mathcal{P}_f)_{\overline{\mathbb{Q}}},\mathbb{Q}_p)) \). Observe now that for every prime \( l \in \mathbb{N} \) we have that \( G_{\mathbb{Q}_l} \subseteq G_{\mathbb{Q}} \), and for all but a finite number of primes the induced representation \( G_{\mathbb{Q}_l} \to \operatorname{GL}_{n_i}(\mathbb{Q}_p) \) is unramified, i.e. it is trivial on the inertia subgroup \( I_{\mathbb{Q}_l} := \ker(G_{\mathbb{Q}_l} \twoheadrightarrow G_{\mathbb{F}_l}) \). This never happens for \( l = p \), which is one of the reasons to consider another cohomology theory (called crystalline cohomology), which is analogous to de Rham cohomology and is more suited for this situation. This rises the question of finding an analogue to de Rham's theorem in this context, which was proved by Gerd Faltings (see here) and can now be seen as a consequence of the work of Bhatt-Morrow-Scholze. We will get back to this.
To motivate the study of perfectoid rings and perfectoid spaces we can go back to Galois representations. More precisely, if \( \rho \colon G_{\mathbb{Q}} \to \operatorname{GL}_n(\mathbb{Q}_p) \) is a continuous group homomorphism which is unramified at finitely many places (i.e. \( I_{\mathbb{Q}_l} \subseteq \ker(\rho) \) for all but finitely many primes \( l \in \mathbb{N} \) ) then Chebotarev's density theorem tells us that \( \rho \) is determined (up to semi-semplification) by the characteristic polynomials of \( \rho([\operatorname{Frob}_l]) \), where \( [\operatorname{Frob}_l] \) is the conjugacy class of Frobenius elements associated to primes lying above the prime \( l \in \mathbb{N} \). These polynomials can be "assembled together" to define the L-function \( L(\rho,s) \) associated to \( \rho \) which determines \( \rho \) up to semi-semplification (see these notes by Takeshi Saito). These functions are the central object of the Langlands program, which aims to relate them to L-functions of a more analytic nature (associated to automorphic forms). Moreover studying their zeros is an incredibly complicated problem, which is (most likely) still open even for the simplest L-function, the Riemann zeta function \( \zeta(s) \) which is associated to the trivial representation of \( G_{\mathbb{Q}} \).
This problem is known to hold for Galois representations which come from varieties over finite fields, as was proved by Pierre Deligne. More precisely if \( \mathfrak{X} \to \operatorname{Spec}(\mathbb{Z}) \) is a scheme of finite type whose structural morphism factors through \( \operatorname{Spec}(\mathbb{F}_p) \) for some prime \( p \in \mathbb{N} \) then the L-function of the Galois representation given by the action of \( G_{\mathbb{Q}} \) on \( H^i_{\text{ét}}(X_{\overline{\mathbb{Q}}},\mathbb{Q}_l) \) (for \( l \neq p \) ) satisfies the Riemann hypothesis, where \( X = \mathfrak{X}_{\mathbb{Q}} \) is the generic fiber of \( \mathfrak{X} \). Thus it might be nice to have a theory which helps us to compare varieties in characteristic zero to varieties in positive characteristic, and this is precisely one of the aims of the theory of perfectoid spaces.(Quasi)-perfectoid rings and spaces
The theory of perfectoid spaces was developed by Peter Scholze in his PhD thesis to put into context Falting's almost purity theorem and to prove the weight monodromy conjecture in certain cases of complete intersection (see this survey paper of Jean-Marc Fontaine and the videos and notes from a workshop at MSRI).In particular, this theory starts with the definition of a perfectoid field, and then defines a perfectoid algebra and a perfectoid space over such a field. We will instead introduce perfectoid rings directly, as it is done in Section 3 of the first paper of Bhatt, Morrow and Scholze. To do so we need to talk about perfect rings, perfections and the period ring \( \mathbb{A}_{\text{inf}} \) defined by Fontaine.
Let \( p \in \mathbb{N} \) be a prime number (which will be fixed in what follows) and \( R \) a ring of characteristic \( p \). Then \( R \) is said to be perfect if the Frobenius map \( R \to R \) defined by \( x \mapsto x^p \) is an isomorphism. Recall in particular that the Frobenius is always a ring map because in positive characteristic we have the freshmen's dream identity \( (x+y)^p = x^p + y^p \).
Let now \( \iota \colon \mathbf{Perf}_{\mathbb{F}_p} \hookrightarrow \mathbf{Alg}_{\mathbb{F}_p} \) denote the full sub-category of perfect rings in characteristic \( p \). Then we have two functors \( (-)^{\text{perf}}, (-)_{\text{perf}} \colon \mathbf{Alg}_{\mathbb{F}_p} \to \mathbf{Perf}_{\mathbb{F}_p} \) which are related to \( \iota \) by the adjunctions \( (-)_{\text{perf}} \dashv \iota \dashv (-)^{\text{perf}} \), and can be defined as \( R^{\text{perf}} := \varprojlim_{\varphi} R \) and \( R_{\text{perf}} := \varinjlim_{\varphi} R \), where \( \varphi \colon R \to R \) is the Frobenius map.
We have finally a tilt functor \( (-)^{\flat} \colon \mathbf{CRing} \to \mathbf{Perf}_{\mathbb{F}_p} \) defined as \( R^{\flat} := (R/p R)^{\text{perf}} \) and it is not difficult to show that \( R^{\flat} \cong \varprojlim_{x \mapsto x^p} R \) as multiplicative monoids (see Lemma 2.0.6 of these notes of Bhargav Bhatt). This identification gives us a multiplicative map \( (-)^{\sharp} \colon R^{\flat} \to R \) by projecting onto the first component of the projective limit. This map clearly becomes a ring homomorphism if we compose it with the quotient map \( R \twoheadrightarrow R/p R \).
Now we can define the functor \( \mathbb{A}_{\text{inf}} \colon \mathbf{CRing} \to \mathbf{CRing} \) as \( \mathbb{A}_{\text{inf}}(R) := W(R^{\flat}) \), where \( W \colon \mathbf{Perf}_{\mathbb{F}_p} \to \mathbf{CRing} \) is the functor which associates to a perfect ring \( R \) of characteristic \( p \) its ring of Witt vectors \( W(R) \).
The construction of Witt vectors can be made very explicit (see these notes of Joseph Rabinoff), but for us it will be sufficient to recall that \( W(R) \) is (up to isomorphism) the unique \( p \)-adically complete ring such that \( p \) is not a zero divisor in \( W(R) \) and \( W(R)/p W(R) \cong R \). Moreover one can show that the quotient map \( W(R) \twoheadrightarrow R \) admits a unique multiplicative section \( [-] \colon R \to W(R) \) which is called the Teichmüller map, and every element \( x \in W(R) \) admits a unique expansion \( x = \sum_{n = 0}^{+\infty} \ [x_n] \, p^n \).
Using this one can prove the universal property of Witt vectors, i.e. the fact that for every \( p \)-adically complete ring \( S \) the map \( \operatorname{Hom}(W(R),S) \to \operatorname{Hom}(R,S/p S) \) obtained by reducing modulo \( p \) is a bijection (see Theorem 6.6 of Rabinoff's notes).
This finally gives us a map \( \Theta \colon \mathbb{A}_{\text{inf}}(R) \to R \) for every \( p \)-adically complete ring \( R \), which is induced by the ring homomorphism \( (-)^{\sharp} \colon R^{\flat} \to R/p R \).
We are now able to define a perfectoid ring as in Definition 3.5 of the first paper of Bhatt, Morrow and Scholze. More precisely, a ring \( R \) is said to be perfectoid (at the prime \( p \)) if it is semi-perfect (i.e. the Frobenius map \( R/p \to R/p \) is surjective), it is \( \pi \)-adically complete for some \( \pi \in R \) with \( \pi^p \mid p \) (which implies that \( R \) is \( p \)-adically complete) and if the kernel of \( \Theta \colon \mathbb{A}_{\text{inf}}(R) \to R \) is principal. We will denote by \( \mathbf{Perfd_p} \hookrightarrow \mathbf{CRing} \) the full subcategory of rings which are perfectoid at the prime \( p \).
Perfectoid rings and topological Hochschild homology
Perfectoid rings are important in the second paper of Bhatt, Morrow and Scholze because the functors \( \pi_{\ast}(\operatorname{THH}(-)^{\wedge p}), \pi_{\ast}(\operatorname{TP}(-)^{\wedge p}), \pi_{\ast}(\operatorname{TC}^{-}(-)^{\wedge p}) \colon \mathbf{CRing} \to \mathbf{CRing} \) can be computed explicitly on \( \mathbf{Perfd_p} \). Here \( \operatorname{THH} \) is topological Hochschild homology, which on \( \mathbb{E}_{\infty} \)-rings (i.e. commutative monoids in spectra) can be described as the initial \( \mathbb{T} \)-equivariant \( \mathbb{E}_{\infty}\)-ring (where \( \mathbb{T} \) is the circle group) with a map \( A \to \operatorname{THH}(A) \). This universal property allows us to endow \( \operatorname{THH}(A) \) with a \( \mathbb{T} \)-equivariant Frobenius map \( \varphi_p \colon \operatorname{THH}(A) \to \operatorname{THH}(A)^{t C_p} \), where \( C_p \subseteq \mathbb{T} \) is the cyclic group with \( p \) elements and \( \operatorname{THH}(A)^{t C_p} \) is the Tate construction. Then one can use \( \operatorname{THH} \) to define the functors \( TP(-) := THH(-)^{t \mathbb{T}} \) and \( TC^{-}(-) := THH(-)^{h \mathbb{T}} \), and one can complete all these \( \mathbb{E}_{\infty} \)-rings at the prime \( p \) (see ) and take the homotopy groups of the result, which gives us the three functors that we had in the beginning. To know more about the (more general) construction of \( \operatorname{THH} \) used in the work of Bhatt, Morrow and Scholze one can look at the preprint "On topological cyclic homology" by Thomas Nikolaus and Peter Scholze.We can now state the main results of Section 6.1 of the second paper of Bhatt, Morrow and Scholze, which computes these functors on perfectoid rings. More precisely, for every perfectoid ring \( R \in \mathbf{Perfd_p} \) we have that \[ \pi_{\ast}(\operatorname{THH}(R)^{\wedge p}) = \mathbb{A}_{\text{inf}}(R)[u] \qquad \pi_{\ast}(\operatorname{TP}(R)^{\wedge p}) = \mathbb{A}_{\text{inf}}(R)[\sigma,\sigma^{-1}] \qquad \pi_{\ast}(\operatorname{TC}^{-}(R)^{\wedge p}) \cong \frac{\mathbb{A}_{\text{inf}}(R)[X,Y]}{(X Y - \xi)} \] where \( u \in \pi_2(\operatorname{THH}(R)^{\wedge p}) \cong \ker(\Theta)/\ker(\Theta)^2 \), \( \sigma \in \pi_2(TP(R)^{\wedge p}) \) and \( \xi \in \ker(\Theta) \) are generators.
These identifications allow us to describe the functors \( \pi_{\ast}(\operatorname{THH}(-)^{\wedge p}), \pi_{\ast}(\operatorname{TP}(-)^{\wedge p}), \pi_{\ast}(\operatorname{TC}^{-}(-)^{\wedge p}) \) on the bigger category \( \mathbf{QSyn}_p \hookrightarrow \mathbf{CRings} \) of quasi-syntomic rings, because they are sheaves for a suitable Grothendieck topology which has the property that every sheaf is determined by its values on the smaller category \( \mathbf{QRSPerfd}_p \hookrightarrow \mathbf{QSyn}_p \) which is closely related to \( \mathbf{Perfd}_p \hookrightarrow \mathbf{QRSPerfd}_p \) (see Proposition 4.30 of the second paper of Bhatt, Morrow and Scholze).
Quasi-syntomic rings
So, how can we define the categories \( \mathbf{QSyn}_p \) and \( \mathbf{QRSPerfd}_p \)? To do so we need to recall that for every map of rings \( A \to B \) the cotangent complex \( L_{B/A} \) is given by \( \Omega_{P_{\bullet}/A} \otimes_{\varepsilon} B \), where \( P_{\bullet} \) is a simplicial polynomial algebra over \( A \) with an augmentation \( \varepsilon \colon P_{\bullet} \to B \) (e.g. we can take the standard resolution \( P_0 = A[B] \), \( P_1 = A[A[B]] \) and so on) and \( \Omega_{P_{\bullet}/A} \) is the module of differentials in the category of simplicial algebras over \( A \).Moreover recall that if \( R \) is a ring and \( C_{\bullet} \in \operatorname{D}(R) \) is a complex of \(R\)-modules we say that \( C_{\bullet} \) has \( p \)-complete Tor amplitude in \( [a,b] \) (for some integers \( a \leq b \) ) if for every \( R/p R \)-module \( M \) the complex \( (C_{\bullet} \otimes_R^{\mathbb{L}} R/p R) \otimes_{R/p R}^{\mathbb{L}} M \) is concentrated in degrees \( a, a+1, \dots, b \).
Using the cotangent complex we can now define a map of rings \( A \to B \) to be quasi-syntomic (at a prime \( p \in \mathbb{N} \) ) if \( A^{\wedge p} \to B^{\wedge p} \) is flat and \( L_{B/A} \) has p-complete Tor amplitude in \( [-1,0] \). The reason for this name is that if \( A \to B \) is quasi-syntomic, \( A \) and \( B \) are Noetherian and \( B \) is of finite type over \( A \) then the map \( A^{\wedge p} \to B^{\wedge p} \) is syntomic, i.e. it's flat, of finite presentation and a local complete intersection.
Moreover we say that a quasi-syntomic map \( A \to B \) is a quasi-syntomic cover if \( A^{\wedge p} \to B^{\wedge p} \) is faithfully flat.
Now a ring \( R \) is said to be quasi-syntomic (at a prime \( p \)) if it is \( p \)-complete, if it has bounded \( p \)-torsion and if \( L_{A/\mathbb{Z}_p} \) has \( p \)-complete Tor amplitude in \( [-1,0] \). We denote by \( \mathbf{QSyn}_p \hookrightarrow \mathbf{CRing} \) the full subcategory of quasi-syntomic rings, and we endow it with the Grothendieck topology whose covering families are quasi-syntomic covers.
Moreover the category \( \mathbf{QRSPerfd}_p \) of quasi-regular, semi-perfectoid rings (at the prime \( p \) ) is the full sub-category of \( \mathbf{QSyn}_p \) whose objects are all the quasi-syntomic rings \( S \) which are semi-perfect and admit a map \( R \to S \) with \( R \in \mathbf{Perfd}_p \).
Observe now that \( \mathbf{Perfd}_p \hookrightarrow \mathbf{QRSPerfd}_p \) because if \( R \) is a perfectoid ring (at the prime \( p \in \mathbb{N} \) then \( R[p^{\infty}] = R[p] \) and \( L_{R/\mathbb{Z}_p} \) has \( p \)-complete Tor amplitude in \( [-1,-1] \). This last observation can be proved by looking at the triangle \( L_{\mathbb{A}_{\text{inf}}(R)/\mathbb{Z}_p} \otimes^{\mathbb{L}}_{\Theta} R \to L_{R/\mathbb{Z}_p} \to L_{R/\mathbb{A}_{\text{inf}}(R)} \) where the first element becomes trivial after \( p \)-completion and \( L_{R/\mathbb{A}_{\text{inf}}(R)} \cong \ker(\Theta)/\ker(\Theta)^2[1] \) because \( \ker(\Theta) \) is generated by a non-zero divisor (see Lemma 3.10 of the first paper of Bhatt, Morrow and Scholze).
As we said, the category \( \mathbf{QRSPerfd}_p \) is defined because one can extend the computations of \( \operatorname{THH} \), \( \operatorname(TP) \) and \( \operatorname{TC}^{-} \) from \( \mathbf{Perfd}_p \) to \( \mathbf{QRSPerfd}_p \), as it is explained in Section 7 of the second paper of Bhatt, Morrow and Scholze.
Perfectoid spaces
In my talk I wanted also to speak a little bit about the general theory of perfectoid spaces, which originates from the wish to upgrade the homeomorphism \( \mathbb{F}_p((T)) \to \mathbb{Q}_p \) which sends \( T \) to \( p \) to a map of topological fields. This was achieved by Fontaine and Jean-Pierre Winterberger, who proved (see here) that the map \( \mathbb{Q}_p(p^{1/p^{\infty}}) \to \mathbb{F}_p((T))(T^{1/p^{\infty}}) \) which sends \( p \) to \( T \) induces an isomorphism of Galois groups \( G_{\mathbb{Q}_p(p^{1/p^{\infty}})} \cong G_{\mathbb{F}_p((T))(T^{1/p^{\infty}})} \). The theory of perfectoid spaces allowed Scholze to generalize this theorem and to put it into a general context.In the original paper, Scholze defines a perfectoid field (at a prime \( p \in \mathbb{N} \) ) as a complete, non-Archimedean field \( K \) with residue characteristic \( p > 0 \) such that \( \lvert K^{\times} \rvert \) is not discrete and \( \mathcal{O}_K := \{ x \in K \colon \lvert x \rvert \leq 1 \} \) is semi-perfect. One can show that this happens if and only if \( \mathcal{O}_K \) is perfectoid in our sense.
More generally, there is a comparison between the notion of a perfectoid Tate ring in the sense of Fontaine and the notion of perfectoid ring in the sense of Bhatt, Morrow and Scholze. Recall that a ring \( R \) is a Tate ring if and only if it is a topological ring for which there exists a sub-ring \( R_0 \subseteq R \) on which the topology is \( \pi \)-adic for some element \( \pi \in R_0 \) for which \( R = R_0[1/\pi] \). In this situation we can say that a subset \( S \subseteq R \) is bounded if \( S \subseteq t^{-n} A_0 \) for some \( n \in \mathbb{N} \), and we can define the subring \( R^{\circ} \subseteq R \) of elements whose set of powers is bounded. With these notions we define a Tate ring \( R \) to be perfectoid (in the sense of Fontaine) if \( R^{\circ} \) is bounded and there is \( \pi \in R \) which is topologically nilpotent such that \( \pi^p \mid p \) and the Frobenius map on \( R^{\circ}/ \pi^p R^{\circ} \) is surjective. Then one can show that if \( R \) is a Tate ring which is perfectoid in Fontaine's sense then every open and integrally closed subring \( R^{\dagger} \subseteq R^{\circ} \) is perfectoid. Moreover, if a Tate ring \( R \) contains a perfectoid bounded sub-ring \( R^{\dagger} \subseteq R^{\circ} \) which is open and integrally closed then \( R \) is perfectoid in Fontaine's sense. Finally, for every perfectoid ring \( R \) which is \( \pi \)-adically complete for some \( \pi \in R \) with \( \pi \mid p \) we have that \( R[1/\pi] \) is a Tate ring and is perfectoid in Fontaine's sense. For the proof of these results see Lemma 3.20 and 3.21 of the first paper of Bhatt, Morrow and Scholze.
Finally, we recall how one can define adic and perfectoid spaces starting from Tate rings. More precisely if \( A \) is a Tate ring and \( A^{\dagger} \subseteq A^{\circ} \) is an open and integrally closed subring we define \( \operatorname{Spa}(A,A^{\dagger}) \) to be the set of all absolute values \( \lvert \cdot \rvert \colon A \to \Gamma \cup \{ 0 \} \) (where \( \Gamma \) is a totally ordered multiplicative abelian group) such that \( \lvert x \rvert \leq 1 \) for all \( x \in A^{\dagger} \) and \( \lvert \cdot \rvert \) is continuous with respect to the order topology on the target, quotiented out by the equivalence relation given by \( \lvert \cdot \rvert_1 \sim \lvert \cdot \rvert_2 \) when \( \lvert x \rvert_1 \geq \lvert y \rvert_1 \) if and only if \( \lvert x \rvert_2 \geq \lvert y \rvert_2 \). This set is given the topology generated by the subsets of the form \( \{ \lvert \cdot \rvert \in \operatorname{Spa}(A,A^{\dagger}) \colon \lvert f \rvert \leq \lvert g \rvert \} \) for \( f, g \in A \).
This topological space is called affinoid, and it's moreover called affinoid perfectoid if \( A \) is perfectoid in Fontaine's sense, or if \( A^{\dagger} \) is perfectoid in the sense of Bhatt, Morrow and Scholze.
An adic space is then defined by glueing these topological spaces, and a perfectoid space is defined by glueing affinoid perfectoids. For the problems given by this glueing (for example, the definition of a sheaf on \( \operatorname{Spa}(A,A^{\dagger}) \) ) see Lecture II and III of these notes by Jared Weinstein and Peter Scholze).
Three of the most surprising applications of the theory of perfectoid spaces are:
- the almost purity theorem, saying that there is an equivalence of étale sites \( X_{ét} \cong X^{\flat}_{ét} \) where the tilt \( (-)^{\flat} \) is defined by glueing the tilt functor that we have on rings;
- the weight monodromy conjecture of Deligne on the Frobenius-eigenvalue decomposition of étale cohomology (see Section 8 of this survey paper of Peter Scholze);
- the direct summand conjecture (proved by Yves André and later on by Bhargav Bhatt), which says that every finite ring extension \( R \subseteq S \) splits if \( R \) is regular (see this survey by André).
Conclusions
In this talk, we managed to define the two categories \( \mathbf{QSyn}_p \) and \( \mathbf{QRSPerfd}_p \) and to state one of the main results of the second paper of Bhatt, Morrow and Scholze concerning the computation of topological Hochschild homology for perfectoid rings. Moreover we recalled very briefly the basic notions and results in the theory of perfectoid spaces.As we have already said, the original plan was to cover also the main properties of the two cohomology theories defined in Bhatt, Morrow and Scholze (one over \( \mathbb{A}_{\text{inf}}(\mathcal{O}_C) \) for a complete, algebraically closed non-Archimedean field \( C \) and the other on \( \mathfrak{S}(\mathcal{O}_K) := W(\mathcal{O}_K/\mathfrak{m}_K)\llbracket z \rrbracket \) for a \( p \)-adic field \( K \) ) and to see how one can "visualize" the ring \( \mathbb{A}_{\text{inf}}(R) \) by means of the curve of Fargues and Fontaine. We will hopefully keep these topics for a subsequent talk!
Comments
Post a Comment