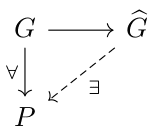Achilles and the tortoise

Hello there! These are notes for the twentieth class of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . In the previous lecture we used the idelic class group \( C_K \) to give the statement of the main theorem of global class field theory. Moreover, we related this group to the "traditional" class group \( \mathfrak{C}_K \) by proving that \[ \mathfrak{C}_K \cong \frac{C_K}{(\widehat{\mathcal{O}_K^{\times}} \cdot \mathbb{I}_{K,\infty}) \cdot K^{\times}}. \] In this lecture we will use this isomorphism to state the main theorem of global class field theory in terms of ideal classes. In order to do so, we need to prove that the groups \( \overline{U}_K^{\mathfrak{m}} \subseteq C_K \) that we defined in the last lecture are of finite index in \( C_K \), which is what we will do in the second section.

Hello there! These are notes for the nineteenth class of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . In the last lecture we defined the ring of adèles \( \mathbb{A}_K \), the group of idèles \( \mathbb{I}_K := \mathbb{A}_K^{\times} \) and the idèle class group \( C_K := \mathbb{I}_K/K^{\times} \) of a global field \( K \). We have moreover seen that we can construct a continuous group homomorphism \( \mathbb{I}_K \to G_K^{\text{ab}} \) by gluing together all the local Artin maps. The biggest deal to complete the proof of the main theorem of global class field theory is then to show that this map is surjective and its kernel contains \( K^{\times} \). Thus, this map induces a global Artin map \( \theta_K \colon C_K \to  G_K^{\text{ab}} \) which in turn induces an isomorphism \( \widehat{C_K} \cong G_K^{\text{ab}} \). This isomorphism will give us a bijective correspondence between open...

Hello there! These are notes for the eighteenth class of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . In the previous lecture we saw that for every local field \( K \) we have a natural isomorphism \( G_K^{\text{ab}} \cong \widehat{K^{\times}} \). This generalizes the isomorphism \( G_{\mathbb{Q}_p}^{\text{ab}} \cong \widehat{\mathbb{Q}_p^{\times}} \) which we proved in the sixteenth lecture as a consequence of the local version of the theorem of Kronecker and Weber. In the same lecture we also proved that \( G_{\mathbb{Q}}^{\text{ab}} \cong \widehat{\mathbb{Z}} \) as a consequence of the global version of the theorem of Kronecker and Weber. Thus it is a natural question to ask if we can generalize this result to an arbitrary number field \( K \). In particular, it would be nice if we could "glue" the local Artin maps \( \theta_{\mathfrak{p}} \colon K_{\mathfrak{p}} \to G_{K_...

Hello there! These are notes for the seventeenth class of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . In the previous lecture we proved the global version of the theorem of Kronecker and Weber, and we have also seen how this theorem enables us to compute the abelian part of the absolute Galois group \( G_{\mathbb{Q}} \). It is now natural to ask: can we do so for every number field \( K \)? More precisely, can we find an analogue of roots of unity which would enable us to characterize abelian extensions of a number field \( K \), and thus to compute the group \( G_K^{\text{ab}} \)? It turns out that the second question has a positive answer, whereas the first question is rather hopeless (apart from one specific case, which we will see in the last week of the course). This last part of the course is thus devoted to compute the abelian group \( G_K^{\text{ab}} \) for every number field \...

Hello there! These are notes for the sixteenth class of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . In the previous lecture we have (almost) proved that every finite abelian extension of \( \mathbb{Q}_p \) is contained in a cyclotomic extension. We will use this local result to prove that the same is true for finite abelian extensions of \( \mathbb{Q} \). This is the famous Theorem of Kronecker and Weber , which was completely proved by David Hilbert in his paper " Ein neuer Beweis des Kroneckerschen Fundamentalsatzes über Abelsche Zahlkörper ". Since the theorem is so old you may guess that Hilbert didn't use (as we do) all the machinery of local fields to prove the theorem. Indeed his proof was only based on ramification theory of local fields. If you want to read a modern version of this simple proof, you can read this paper (and the correction to it ) of Marvin J. Gre...

Hello there! These are notes for the fifteenth class of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . In the previous lecture we have defined the ramification filtration of a finite, Galois extension of complete, discretely valued fields. This filtration gives us a way of studying the Galois group of any extension of complete, discretely valued fields. In this lecture we will concentrate on Galois extensions of a local field that are abelian , i.e. the Galois group is commutative. In particular we will see that every (tamely ramified) abelian extension of \( \mathbb{Q}_{p} \) is contained in a cyclotomic extension. In order to do so, we will need a lemma which will enable us to kill the ramification in an extension of valued fields after changing the base field: this is the so-called Abhyankhar's lemma .

Hello there! These are notes for the fourteenth class of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . In the previous lecture we have seen how every extension \( (K,\phi) \hookrightarrow (L,\psi) \) of complete, non-Archimedean, discretely valued fields can be split into an unramified and a totally ramified extension. We have seen moreover that unramified extensions correspond bijectively to separable extensions of the residue field and totally ramified extensions correspond to Eisenstein polynomials. In this lecture we will see how the presence of the absolute values allows us to define a filtration on the Galois group of any Galois extension \( (K,\phi) \hookrightarrow (L,\psi) \) of complete, non-Archimedean, discretely valued fields. This filtration will be really useful in the following lectures, to prove the theorem of Kronecker and Weber.

Hello there! These are notes for the thirteenth class of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . In the previous lecture we discussed extensions of absolute values. We have seen in particular that for every valued field \( (K,\phi) \) and every finite, separable extension \( K \subseteq L \) there exist only a finite number of absolute values \( \psi \colon L \to \mathbb{R}_{\geq 0} \) which extend \( \phi \). Given such an absolute value \( \psi \) we have also defined the ramification index \( e(\psi \mid \phi) \) and the inertia index \( f(\psi \mid \phi) \) which measure how "close" the two absolute values are, in two different ways. In this lecture we will concentrate on extensions of complete, discretely valued fields which are either unramified , i.e. \( e(\psi \mid \phi) = 1 \) or totally ramified , i.e.\( f(\psi \mid \phi) = 1 \). We will prove that all the exte...

Hello there! These are notes for the twelfth class of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . In the previous lecture we have seen two useful applications of completeness: Hensel's lemma , which allows us to solve equations in complete fields by solving them in their residue fields, and a characterization of norms on finite dimensional vector spaces over complete fields. The aim of this lecture is to use the second result as a starting point to study the theory of the extensions of absolute values to an algebraic extension. We have already seen in the second lecture that if we have a field extension \( K \hookrightarrow L \) and an absolute value \( \psi \colon L \to \mathbb{R}_{\geq 0} \) we can restrict it to an absolute value \( \phi \colon K \to \mathbb{R}_{\geq 0} \). Suppose now that we have an absolute value \( \phi \colon K \to \mathbb{R}_{\geq 0} \). Can we exten...

Hello there! These are notes for the eleventh class of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . In the past lectures we have seen a lot of complete fields. In particular, we have seen in the fourth lecture that every complete Archimedean field is isomorphic to a finite extension of \( \mathbb{R} \), and we have seen in the ninth lecture that every non-Archimedean complete field which is discretely valued and whose residue field is finite is either a finite extension of \( \mathbb{Q}_p \) or a finite extension of \( \mathbb{F}_p((T)) \). We have seen moreover in the tenth lecture that we can describe these fields as fields of Laurent series in \( p \) and in \( T \) respectively (with the important difference that in \( \mathbb{Q}_p \) we have to sum with carrying ) or as fraction fields of inverse limits of finite rings.

Hello there! These are notes for the ninth class of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . In the previous lecture we have given a complete characterization of non-Archimedean fields which are locally compact . In particular, we have seen that they are all finite extensions of \( \mathbb{Q}_p \) or \( \mathbb{F}_p((T)) \). Today we are going to study more these two fields, giving an alternative description of them which uses inverse limits .

Hello there! These are notes for the ninth class of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . In the previous lectures we have analyzed the set \( \Sigma_K \) of places of a field \( K \), and we have completely characterized it when \( K \) is a number field. In order to do so we defined in the fourth lecture the notion of completion of a valued field \( (K,\phi) \) and we have seen that every complete, Archimedean field is isomorphic to \( (\mathbb{R},\lvert \cdot \rvert) \) or to \( (\mathbb{C},\lVert \cdot \rVert) \). So, what about the non-Archimedean case? Do we have a similar classification result? The answer is a resounding no! More precisely, we have an infinite number of non-Archimedean complete fields which are not isomorphic, as we will see by the end of the lecture.