TANT 16 - From local to global Kronecker-Weber
Hello there! These are notes for the sixteenth class of the course "Topics in algebra and number theory" held in Block 4 of the academic year 2017/18 at the University of Copenhagen.
In the previous lecture we have (almost) proved that every finite abelian extension of \( \mathbb{Q}_p \) is contained in a cyclotomic extension. We will use this local result to prove that the same is true for finite abelian extensions of \( \mathbb{Q} \). This is the famous Theorem of Kronecker and Weber, which was completely proved by David Hilbert in his paper "Ein neuer Beweis des Kroneckerschen Fundamentalsatzes über Abelsche Zahlkörper". Since the theorem is so old you may guess that Hilbert didn't use (as we do) all the machinery of local fields to prove the theorem. Indeed his proof was only based on ramification theory of local fields. If you want to read a modern version of this simple proof, you can read this paper (and the correction to it) of Marvin J. Greenberg.
Before proving the global Kronecker-Weber theorem we need to find a relationship between Galois groups of fields and Galois groups of their completions, which is the content of next section.
Exercise 2 Prove that \( \mathfrak{D}(\phi,G) \) is indeed a subgroup of \( G \).
Proposition 3 Let \( (K,\phi) \) be a complete field which is not algebraically closed, and let \( G \leq \operatorname{Aut}_{\mathbf{Fields}}(K) \). Then \( \mathfrak{D}(\phi,G) = G \).
Proof Observe first of all that for every \( \sigma \in G \) the map \( \phi \circ \sigma \colon K \to \mathbb{R}_{\geq 0} \) is another absolute value on \( K \). It is also easy to prove that \( K \) is complete with respect to \( \phi \circ \sigma \), and thus we can apply Schmidt's theorem (see Theorem 1.19 of these notes by Pete L. Clark) to see that \( \phi \circ \sigma \) must be equivalent to \( \phi \). Since every field automorphism fixes the prime subfield of a field (see this question on Math StackExchange) this implies that \( \phi \circ \sigma = \phi \), and thus that \( \mathfrak{D}(\phi,G) = G \). Q.E.D.
We will study decomposition groups especially in the case when \( G = \operatorname{Gal}(L/K) \leq \operatorname{Aut}_{\mathbf{Fields}}(L) \) is the Galois group of some Galois extension of valued fields \( (K,\phi) \subseteq (L,\psi) \). In this case we will write \( \mathfrak{D}(L \mid K) := \mathfrak{D}(\psi,\operatorname{Gal}(L/K)) \).
Lemma 4 Let \( (K,\phi) \subseteq (L,\psi) \) be a Galois extension of valued fields. Then the extension \( K_{\phi} \subseteq L_{\psi} \) is Galois with Galois group isomorphic to \( \mathfrak{D}(L \mid K) \).
Proof Consider the diagram on the right. We know by hypothesis that \( K \subseteq L \) is Galois and thus \( L \cap K_{\phi} \subseteq L \) is also Galois and thus \( K_{\phi} \subseteq L_{\psi} \) is Galois, as a consequence of the "diamond theorem" in Galois theory (see for example Proposition 7.14 of these notes by James S. Milne). Moreover the same theorem tells us that \( \operatorname{Gal}(L_{\psi}/K_{\phi}) \cong \operatorname{Gal}(L/L \cap K_{\phi}) \) by the restriction map. Finally we can apply Proposition 3 to see that \( \Psi(\sigma(x)) = \Psi(x) \) for all \( x \in L_{\psi} \) and \( \sigma \in \operatorname{Gal}(L_{\psi}/K_{\phi}) \) (here \( \Psi \) is the extension of \( \psi \) to the completion \( L_{\psi} \) ). This implies that \( \operatorname{Gal}(L/L \cap K_{\phi}) \leq \mathfrak{D}(L \mid K) \). To conclude take \( \sigma \in \mathfrak{D}(L \mid K) \) and observe that we can define a new automorphism \( \widetilde{\sigma} \colon L_{\psi} \to L_{\psi} \) by setting \( \widetilde{\sigma}(x) := \lim_{n \to +\infty} \sigma(x_n) \) where \( x \in L_{\psi} \) and \( \{ x_n \} \) is a sequence of elements of \( L \) which converges to \( x \). The fact that \( \sigma \in \mathfrak{D}(L \mid K) \) allows us to show that \( \widetilde{\sigma} \) is well defined and that fixes \( K_{\phi} \), and it is trivial to observe that \( \widetilde{\sigma} \) coincides with \( \sigma \) on \( L \). Thus \( \mathfrak{D}(L \mid K) \leq \operatorname{Gal}(L/L \cap K_{\phi}) \) and we get an isomorphism \( \mathfrak{D}(L \mid K) \cong \operatorname{Gal}(L_{\psi}/K_{\phi}) \) as desired. Q.E.D.
Remark 5 Recall that if \( K \subseteq L \) is an extension of number fields and \( \mathfrak{p} \subseteq \mathcal{O}_K \) and \( \mathfrak{P} \subseteq \mathcal{O}_L \) are prime ideals we define \( e(\mathfrak{P} \mid \mathfrak{p}) \in \mathbb{N} \) as the maximum power of \( \mathfrak{P} \) which divides \( \mathfrak{p} \mathcal{O}_K \). We say that \( \mathfrak{p} \) ramifies in \( L \) if there exists \( \mathfrak{P} \subseteq \mathcal{O}_L \) such that \( e(\mathfrak{P} \mid \mathfrak{p}) \geq 2 \). If the extension \( K \subseteq L \) is Galois we define also an inertia subgroup \[ I(\mathfrak{P} \mid \mathfrak{p}) := \ker\left( \mathfrak{D}(\mathfrak{P}/\mathfrak{p}) \to \operatorname{Gal}\left(\frac{\mathcal{O}_L}{\mathfrak{P}} \ / \ \frac{\mathcal{O}_K}{\mathfrak{p}}\right) \right) \] where \( \mathfrak{D}(\mathfrak{P}/\mathfrak{p}) := \{ \sigma \in \operatorname{Gal}(L/K) \mid \sigma(\mathfrak{P}) = \mathfrak{P} \} \) is the decomposition group relative to the prime \( \mathfrak{P} \), which coincides with \( \mathfrak{D}(\lvert \cdot \rvert_\mathfrak{P}, \operatorname{Gal}(L/K)) \). It is easy to observe that \( I(\mathfrak{P} \mid \mathfrak{p}) \subseteq \mathfrak{D}(\lvert \cdot \rvert_{\mathfrak{P}},\operatorname{Gal}(L/K)) \) and that under the identification described in Lemma 4 this inertia group corresponds to \( I(L_{\mathfrak{P}} \mid K_{\mathfrak{p}}) \). Moreover we have that \( \# I(\mathfrak{P} \mid \mathfrak{p}) = e(\mathfrak{P} \mid \mathfrak{p}) \), and in particular the extension \( K \subseteq L^{I(\mathfrak{P} \mid \mathfrak{p})} \) is unramified at \( \mathfrak{p} \).
Example 6 Let \( p \in \mathbb{N} \) be a prime and \( r \in \mathbb{N} \). Then the only prime which ramifies in the extension \( \mathbb{Q} \subseteq \mathbb{Q}(\zeta_{p^r}) \) is precisely \( p \), and we have that \( p \mathbb{Z}[\zeta_{p^r}] = (1 - \zeta_{p^r})^{p^{r - 1} (p - 1)} \). It follows that for every \( n \in \mathbb{N} \) a prime ramifies in the extension \( \mathbb{Q} \subseteq \mathbb{Q}(\zeta_n) \) if and only if it divides \( n \). For a proof of these results see these notes of Ian Kiming or Theorem 3.12 of these notes by Peter Stevenhagen.
Theorem 7 Let \( \mathbb{Q} \subseteq K \) be a finite, Galois extension and suppose that \( \operatorname{Gal}(K/\mathbb{Q}) \) is abelian. Then there exists \( n \in \mathbb{N} \) such that \( K \subseteq \mathbb{Q}(\zeta_n) \).
Proof Let \( \{ p_1,\dots,p_r \} \) be the collection of primes which ramify in the extension \( \mathbb{Q} \subseteq K \), which is finite because it consists precisely of those primes which divide the discriminant of \( K \) (see Definition 4.4 and Theorem 4.14 of these notes by Peter Stevenhagen). Choose prime ideals \( \{ \mathfrak{p}_1,\dots,\mathfrak{p}_r \} \) of \( \mathcal{O}_L \) such that \( \mathfrak{p}_j \cap \mathbb{Z} = p_j \, \mathbb{Z} \) for all \( j \in \{ 1,\dots,r \} \) (it does not matter which primes we choose). Then we know from Lemma 4 that for every \( j \in \{ 1,\dots,r \} \) the extension \( \mathbb{Q}_{p_j} \subseteq K_{\mathfrak{p_j}} \) is abelian, and thus we know by Corollary 11 of the previous lecture that there exist \( \{ n_1, \dots, n_r \} \subseteq \mathbb{N} \) such that \( K_{\mathfrak{p_j}} \subseteq \mathbb{Q}_{p_j}(\zeta_{n_j}) \) for all \( j \in \{ 1,\dots,r \} \). Let now \( a_j := v_p(n_j) \) be the maximal power of \( p \) which divides \( n_j \). We claim that \( K \subseteq \mathbb{Q}(\zeta_n) \) where \( n := p_1^{a_1} \cdots p_r^{a_r} \).
Indeed observe that proving this is equivalent to prove that \( K(\zeta_n) = \mathbb{Q}(\zeta_n) \). Observe also that the primes which ramify in the extension \( \mathbb{Q} \subseteq K(\zeta_n) \) are precisely \( \{ p_1,\dots,p_r \} \) (see Lemma 3.3.30 of the book "Number Theory I" by Henry Cohen). Let now \( \{ \mathfrak{P}_1,\dots,\mathfrak{P}_r \} \) be primes of \( \mathcal{O}_{K(\zeta_n)} \) lying above \( \{ p_1,\dots,p_r \} \) and observe that \( e(\mathfrak{P}_j \mid p_j) = p_j^{a_j - 1} (p_j - 1) \) because we can write \( n_j = p_j^{a_j} m_j \) with \( p \nmid m_j \) and we have that \( K(\zeta_n)_{\mathfrak{P}_j} = \mathbb{Q}_{p_j}(\zeta_{p_j^{a_j}}) \mathbb{Q}_{p_j}(\zeta_{m_j}) \) where \( \mathbb{Q}_{p_j} \subseteq \mathbb{Q}_{p_j}(\zeta_{p_j^{a_j}}) \) is totally ramified and \( \mathbb{Q}_{p_j} \subseteq \mathbb{Q}_{p_j}(\zeta_{m_j}) \) is unramified (see Example 7 of the previous lecture).
Let now \( I := I(\mathfrak{P}_1 \mid p_1) \cdots I(\mathfrak{P}_r \mid p_r) \leq \operatorname{Gal}(K(\zeta_n)/\mathbb{Q}) \) be the product of all the inertia groups relative to the primes \( \{ \mathfrak{P}_1,\dots,\mathfrak{P}_r \} \). Applying what we have seen in Remark 5 we see that the extension \( \mathbb{Q} \subseteq K(\zeta_n)^{I} \) is unramified at all (finite) primes, and this implies that \( K(\zeta_n)^{I} = \mathbb{Q} \) (see Corollary 5.11 of these notes by Peter Stevenhagen). This implies that \( I = \operatorname{Gal}(K(\zeta_n)/\mathbb{Q}) \) and thus in particular that \( \# I = [K(\zeta_n) \colon \mathbb{Q}] \). Finally, we know from the previous paragraph that \[ [K(\zeta_n) \colon \mathbb{Q}] = \# I = \prod_{j = 1}^r p_j^{a_j - 1} (p_j - 1) = \varphi(n) = [\mathbb{Q}(\zeta_n) \colon \mathbb{Q}] \] where \( \varphi \) is Euler's totient function. Thus \( K(\zeta_n) = \mathbb{Q}(\zeta_n) \) and we can conclude that \( K \subseteq \mathbb{Q}(\zeta_n) \). Q.E.D.
Using the previous theorem we can deduce something about the abelian part of the absolute Galois group. Recall that the absolute Galois group \( G_{\mathbb{Q}} \) is defined to be the Galois group of the extension \( \mathbb{Q} \subseteq \overline{\mathbb{Q}} \), where \( \overline{\mathbb{Q}} \) is any algebraic closure of \( \mathbb{Q} \). Using the fundamental theorem of Galois theory (see Theorem 7.12 of these notes by James S. Milne) we see that the abelian part of \( G_{\mathbb{Q}} \) can also be described as \( G_{\mathbb{Q}}^{\text{ab}} = \operatorname{Gal}(\mathbb{Q}^{\text{ab}} / \mathbb{Q}) \), where \( \mathbb{Q} \subseteq \mathbb{Q}^{\text{ab}} \subseteq \overline{\mathbb{Q}} \) is the maximal Galois extension of \( \mathbb{Q} \) whose Galois group is abelian.
Corollary 8 We have that \( G_{\mathbb{Q}}^{\text{ab}} \cong \widehat{\mathbb{Z}}^{\times} := \varprojlim_{n \in \mathbb{N}} (\mathbb{Z}/n \mathbb{Z})^{\times} \).
Proof Observe that \( \mathbb{Q}^{\text{ab}} \) is the union of all the finite abelian extensions of \( \mathbb{Q} \). Thus, using Theoerm 7, we get that \[ \mathbb{Q}^{\text{ab}} = \varinjlim_{n \in \mathbb{N}} \mathbb{Q}(\zeta_n) \] and this implies (see Example 7.24 of these notes by James S. Milne) that \[ G_{\mathbb{Q}}^{\text{ab}} = \operatorname{Gal}(\mathbb{Q}^{\text{ab}} / \mathbb{Q}) = \varprojlim_{n \in \mathbb{N}} \operatorname{Gal}(\mathbb{Q}(\zeta_n)/ \mathbb{Q}) \cong \varprojlim_{n \in \mathbb{N}} (\mathbb{Z}/n \mathbb{Z})^{\times} = \widehat{\mathbb{Z}}^{\times} \] which is what we wanted to prove. Q.E.D.
This corollary has also a counterpart for \( \mathbb{Q}_p \), which is proved in the same way using the local version of the theorem of Kronecker and Weber.
Corollary 9 We have that \( G_{\mathbb{Q_p}}^{\text{ab}} \cong \mathbb{Z}_p^{\times} \times \widehat{\mathbb{Z}}^{\times} \).
The next lectures will deal with the problem of finding a generalization of Corollary 8 to number fields. In order to prove this, we will first of all generalize Corollary 9 to general \( p \)-adic fields and then we will assemble together all the information to get the generalization of Corollary 8.
In the previous lecture we have (almost) proved that every finite abelian extension of \( \mathbb{Q}_p \) is contained in a cyclotomic extension. We will use this local result to prove that the same is true for finite abelian extensions of \( \mathbb{Q} \). This is the famous Theorem of Kronecker and Weber, which was completely proved by David Hilbert in his paper "Ein neuer Beweis des Kroneckerschen Fundamentalsatzes über Abelsche Zahlkörper". Since the theorem is so old you may guess that Hilbert didn't use (as we do) all the machinery of local fields to prove the theorem. Indeed his proof was only based on ramification theory of local fields. If you want to read a modern version of this simple proof, you can read this paper (and the correction to it) of Marvin J. Greenberg.
Before proving the global Kronecker-Weber theorem we need to find a relationship between Galois groups of fields and Galois groups of their completions, which is the content of next section.
The decomposition group
Definition 1 Let \( (K,\phi) \) be a valued field, and let \( G \leq \operatorname{Aut}_{\mathbf{Fields}}(K) \) be a group of field automorphisms of \( K \). We define the decomposition group of \( \phi \) with respect to \( G \) as \[ \mathfrak{D}(\phi,G) = \{ \sigma \in G \mid \phi(\sigma(x)) = \phi(x), \ \text{for all} \ x \in K \} \]Exercise 2 Prove that \( \mathfrak{D}(\phi,G) \) is indeed a subgroup of \( G \).
Proposition 3 Let \( (K,\phi) \) be a complete field which is not algebraically closed, and let \( G \leq \operatorname{Aut}_{\mathbf{Fields}}(K) \). Then \( \mathfrak{D}(\phi,G) = G \).
Proof Observe first of all that for every \( \sigma \in G \) the map \( \phi \circ \sigma \colon K \to \mathbb{R}_{\geq 0} \) is another absolute value on \( K \). It is also easy to prove that \( K \) is complete with respect to \( \phi \circ \sigma \), and thus we can apply Schmidt's theorem (see Theorem 1.19 of these notes by Pete L. Clark) to see that \( \phi \circ \sigma \) must be equivalent to \( \phi \). Since every field automorphism fixes the prime subfield of a field (see this question on Math StackExchange) this implies that \( \phi \circ \sigma = \phi \), and thus that \( \mathfrak{D}(\phi,G) = G \). Q.E.D.
We will study decomposition groups especially in the case when \( G = \operatorname{Gal}(L/K) \leq \operatorname{Aut}_{\mathbf{Fields}}(L) \) is the Galois group of some Galois extension of valued fields \( (K,\phi) \subseteq (L,\psi) \). In this case we will write \( \mathfrak{D}(L \mid K) := \mathfrak{D}(\psi,\operatorname{Gal}(L/K)) \).
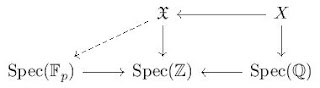
Lemma 4 Let \( (K,\phi) \subseteq (L,\psi) \) be a Galois extension of valued fields. Then the extension \( K_{\phi} \subseteq L_{\psi} \) is Galois with Galois group isomorphic to \( \mathfrak{D}(L \mid K) \).
Proof Consider the diagram on the right. We know by hypothesis that \( K \subseteq L \) is Galois and thus \( L \cap K_{\phi} \subseteq L \) is also Galois and thus \( K_{\phi} \subseteq L_{\psi} \) is Galois, as a consequence of the "diamond theorem" in Galois theory (see for example Proposition 7.14 of these notes by James S. Milne). Moreover the same theorem tells us that \( \operatorname{Gal}(L_{\psi}/K_{\phi}) \cong \operatorname{Gal}(L/L \cap K_{\phi}) \) by the restriction map. Finally we can apply Proposition 3 to see that \( \Psi(\sigma(x)) = \Psi(x) \) for all \( x \in L_{\psi} \) and \( \sigma \in \operatorname{Gal}(L_{\psi}/K_{\phi}) \) (here \( \Psi \) is the extension of \( \psi \) to the completion \( L_{\psi} \) ). This implies that \( \operatorname{Gal}(L/L \cap K_{\phi}) \leq \mathfrak{D}(L \mid K) \). To conclude take \( \sigma \in \mathfrak{D}(L \mid K) \) and observe that we can define a new automorphism \( \widetilde{\sigma} \colon L_{\psi} \to L_{\psi} \) by setting \( \widetilde{\sigma}(x) := \lim_{n \to +\infty} \sigma(x_n) \) where \( x \in L_{\psi} \) and \( \{ x_n \} \) is a sequence of elements of \( L \) which converges to \( x \). The fact that \( \sigma \in \mathfrak{D}(L \mid K) \) allows us to show that \( \widetilde{\sigma} \) is well defined and that fixes \( K_{\phi} \), and it is trivial to observe that \( \widetilde{\sigma} \) coincides with \( \sigma \) on \( L \). Thus \( \mathfrak{D}(L \mid K) \leq \operatorname{Gal}(L/L \cap K_{\phi}) \) and we get an isomorphism \( \mathfrak{D}(L \mid K) \cong \operatorname{Gal}(L_{\psi}/K_{\phi}) \) as desired. Q.E.D.
The theorem of Kronecker and Weber
Using the comparison between local and global Galois groups given by Lemma 4 we are now able to prove the global version of the theorem of Kronecker and Weber. Before doing that, we need a little refresh on the ramification of primes in cyclotomic fields.Remark 5 Recall that if \( K \subseteq L \) is an extension of number fields and \( \mathfrak{p} \subseteq \mathcal{O}_K \) and \( \mathfrak{P} \subseteq \mathcal{O}_L \) are prime ideals we define \( e(\mathfrak{P} \mid \mathfrak{p}) \in \mathbb{N} \) as the maximum power of \( \mathfrak{P} \) which divides \( \mathfrak{p} \mathcal{O}_K \). We say that \( \mathfrak{p} \) ramifies in \( L \) if there exists \( \mathfrak{P} \subseteq \mathcal{O}_L \) such that \( e(\mathfrak{P} \mid \mathfrak{p}) \geq 2 \). If the extension \( K \subseteq L \) is Galois we define also an inertia subgroup \[ I(\mathfrak{P} \mid \mathfrak{p}) := \ker\left( \mathfrak{D}(\mathfrak{P}/\mathfrak{p}) \to \operatorname{Gal}\left(\frac{\mathcal{O}_L}{\mathfrak{P}} \ / \ \frac{\mathcal{O}_K}{\mathfrak{p}}\right) \right) \] where \( \mathfrak{D}(\mathfrak{P}/\mathfrak{p}) := \{ \sigma \in \operatorname{Gal}(L/K) \mid \sigma(\mathfrak{P}) = \mathfrak{P} \} \) is the decomposition group relative to the prime \( \mathfrak{P} \), which coincides with \( \mathfrak{D}(\lvert \cdot \rvert_\mathfrak{P}, \operatorname{Gal}(L/K)) \). It is easy to observe that \( I(\mathfrak{P} \mid \mathfrak{p}) \subseteq \mathfrak{D}(\lvert \cdot \rvert_{\mathfrak{P}},\operatorname{Gal}(L/K)) \) and that under the identification described in Lemma 4 this inertia group corresponds to \( I(L_{\mathfrak{P}} \mid K_{\mathfrak{p}}) \). Moreover we have that \( \# I(\mathfrak{P} \mid \mathfrak{p}) = e(\mathfrak{P} \mid \mathfrak{p}) \), and in particular the extension \( K \subseteq L^{I(\mathfrak{P} \mid \mathfrak{p})} \) is unramified at \( \mathfrak{p} \).
Example 6 Let \( p \in \mathbb{N} \) be a prime and \( r \in \mathbb{N} \). Then the only prime which ramifies in the extension \( \mathbb{Q} \subseteq \mathbb{Q}(\zeta_{p^r}) \) is precisely \( p \), and we have that \( p \mathbb{Z}[\zeta_{p^r}] = (1 - \zeta_{p^r})^{p^{r - 1} (p - 1)} \). It follows that for every \( n \in \mathbb{N} \) a prime ramifies in the extension \( \mathbb{Q} \subseteq \mathbb{Q}(\zeta_n) \) if and only if it divides \( n \). For a proof of these results see these notes of Ian Kiming or Theorem 3.12 of these notes by Peter Stevenhagen.
Theorem 7 Let \( \mathbb{Q} \subseteq K \) be a finite, Galois extension and suppose that \( \operatorname{Gal}(K/\mathbb{Q}) \) is abelian. Then there exists \( n \in \mathbb{N} \) such that \( K \subseteq \mathbb{Q}(\zeta_n) \).
Proof Let \( \{ p_1,\dots,p_r \} \) be the collection of primes which ramify in the extension \( \mathbb{Q} \subseteq K \), which is finite because it consists precisely of those primes which divide the discriminant of \( K \) (see Definition 4.4 and Theorem 4.14 of these notes by Peter Stevenhagen). Choose prime ideals \( \{ \mathfrak{p}_1,\dots,\mathfrak{p}_r \} \) of \( \mathcal{O}_L \) such that \( \mathfrak{p}_j \cap \mathbb{Z} = p_j \, \mathbb{Z} \) for all \( j \in \{ 1,\dots,r \} \) (it does not matter which primes we choose). Then we know from Lemma 4 that for every \( j \in \{ 1,\dots,r \} \) the extension \( \mathbb{Q}_{p_j} \subseteq K_{\mathfrak{p_j}} \) is abelian, and thus we know by Corollary 11 of the previous lecture that there exist \( \{ n_1, \dots, n_r \} \subseteq \mathbb{N} \) such that \( K_{\mathfrak{p_j}} \subseteq \mathbb{Q}_{p_j}(\zeta_{n_j}) \) for all \( j \in \{ 1,\dots,r \} \). Let now \( a_j := v_p(n_j) \) be the maximal power of \( p \) which divides \( n_j \). We claim that \( K \subseteq \mathbb{Q}(\zeta_n) \) where \( n := p_1^{a_1} \cdots p_r^{a_r} \).
Indeed observe that proving this is equivalent to prove that \( K(\zeta_n) = \mathbb{Q}(\zeta_n) \). Observe also that the primes which ramify in the extension \( \mathbb{Q} \subseteq K(\zeta_n) \) are precisely \( \{ p_1,\dots,p_r \} \) (see Lemma 3.3.30 of the book "Number Theory I" by Henry Cohen). Let now \( \{ \mathfrak{P}_1,\dots,\mathfrak{P}_r \} \) be primes of \( \mathcal{O}_{K(\zeta_n)} \) lying above \( \{ p_1,\dots,p_r \} \) and observe that \( e(\mathfrak{P}_j \mid p_j) = p_j^{a_j - 1} (p_j - 1) \) because we can write \( n_j = p_j^{a_j} m_j \) with \( p \nmid m_j \) and we have that \( K(\zeta_n)_{\mathfrak{P}_j} = \mathbb{Q}_{p_j}(\zeta_{p_j^{a_j}}) \mathbb{Q}_{p_j}(\zeta_{m_j}) \) where \( \mathbb{Q}_{p_j} \subseteq \mathbb{Q}_{p_j}(\zeta_{p_j^{a_j}}) \) is totally ramified and \( \mathbb{Q}_{p_j} \subseteq \mathbb{Q}_{p_j}(\zeta_{m_j}) \) is unramified (see Example 7 of the previous lecture).
Let now \( I := I(\mathfrak{P}_1 \mid p_1) \cdots I(\mathfrak{P}_r \mid p_r) \leq \operatorname{Gal}(K(\zeta_n)/\mathbb{Q}) \) be the product of all the inertia groups relative to the primes \( \{ \mathfrak{P}_1,\dots,\mathfrak{P}_r \} \). Applying what we have seen in Remark 5 we see that the extension \( \mathbb{Q} \subseteq K(\zeta_n)^{I} \) is unramified at all (finite) primes, and this implies that \( K(\zeta_n)^{I} = \mathbb{Q} \) (see Corollary 5.11 of these notes by Peter Stevenhagen). This implies that \( I = \operatorname{Gal}(K(\zeta_n)/\mathbb{Q}) \) and thus in particular that \( \# I = [K(\zeta_n) \colon \mathbb{Q}] \). Finally, we know from the previous paragraph that \[ [K(\zeta_n) \colon \mathbb{Q}] = \# I = \prod_{j = 1}^r p_j^{a_j - 1} (p_j - 1) = \varphi(n) = [\mathbb{Q}(\zeta_n) \colon \mathbb{Q}] \] where \( \varphi \) is Euler's totient function. Thus \( K(\zeta_n) = \mathbb{Q}(\zeta_n) \) and we can conclude that \( K \subseteq \mathbb{Q}(\zeta_n) \). Q.E.D.
Using the previous theorem we can deduce something about the abelian part of the absolute Galois group. Recall that the absolute Galois group \( G_{\mathbb{Q}} \) is defined to be the Galois group of the extension \( \mathbb{Q} \subseteq \overline{\mathbb{Q}} \), where \( \overline{\mathbb{Q}} \) is any algebraic closure of \( \mathbb{Q} \). Using the fundamental theorem of Galois theory (see Theorem 7.12 of these notes by James S. Milne) we see that the abelian part of \( G_{\mathbb{Q}} \) can also be described as \( G_{\mathbb{Q}}^{\text{ab}} = \operatorname{Gal}(\mathbb{Q}^{\text{ab}} / \mathbb{Q}) \), where \( \mathbb{Q} \subseteq \mathbb{Q}^{\text{ab}} \subseteq \overline{\mathbb{Q}} \) is the maximal Galois extension of \( \mathbb{Q} \) whose Galois group is abelian.
Corollary 8 We have that \( G_{\mathbb{Q}}^{\text{ab}} \cong \widehat{\mathbb{Z}}^{\times} := \varprojlim_{n \in \mathbb{N}} (\mathbb{Z}/n \mathbb{Z})^{\times} \).
Proof Observe that \( \mathbb{Q}^{\text{ab}} \) is the union of all the finite abelian extensions of \( \mathbb{Q} \). Thus, using Theoerm 7, we get that \[ \mathbb{Q}^{\text{ab}} = \varinjlim_{n \in \mathbb{N}} \mathbb{Q}(\zeta_n) \] and this implies (see Example 7.24 of these notes by James S. Milne) that \[ G_{\mathbb{Q}}^{\text{ab}} = \operatorname{Gal}(\mathbb{Q}^{\text{ab}} / \mathbb{Q}) = \varprojlim_{n \in \mathbb{N}} \operatorname{Gal}(\mathbb{Q}(\zeta_n)/ \mathbb{Q}) \cong \varprojlim_{n \in \mathbb{N}} (\mathbb{Z}/n \mathbb{Z})^{\times} = \widehat{\mathbb{Z}}^{\times} \] which is what we wanted to prove. Q.E.D.
This corollary has also a counterpart for \( \mathbb{Q}_p \), which is proved in the same way using the local version of the theorem of Kronecker and Weber.
Corollary 9 We have that \( G_{\mathbb{Q_p}}^{\text{ab}} \cong \mathbb{Z}_p^{\times} \times \widehat{\mathbb{Z}}^{\times} \).
The next lectures will deal with the problem of finding a generalization of Corollary 8 to number fields. In order to prove this, we will first of all generalize Corollary 9 to general \( p \)-adic fields and then we will assemble together all the information to get the generalization of Corollary 8.
Conclusions and references
In this lecture we managed to:- relate local and global Galois groups using the decomposition group;
- prove the theorem of Kronecker and Weber using the local version of this theorem that we proved in the previous lecture;
- describe the groups \( G_{\mathbb{Q}}^{\text{ab}} \) and \( G_{\mathbb{Q_p}}^{\text{ab}} \).
- Section 6 of these notes by Peter Stevenhagen;
- these notes by Andrew Sutherland;
- Chapter 14 of the book "Introduction to Cyclotomic Fields" by Lawrence C. Washington.


Comments
Post a Comment