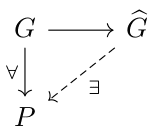Posts

A (not quite) perfect(oid) talk

-
Image
Hi all! These are notes for a talk that I gave at a seminar on the work of Bhargav Bhatt , Matthew Morrow and Peter Scholze ( I and II ) organized in Copenhagen by Elden Elmanto . The aim of this talk was to introduce the main results of the two papers, and the categories \( \mathbf{QSyn} \) and \( \mathbf{QRSPerfd} \) that appear in the second paper. As the discussions went on for a long time, I managed only to achieve this second task, but I will post here the original notes for the talk, which might be used for a follow-up talk later on. Disclaimer : these notes have not been fully revised and most likely contain a wide variety of errors, misprints and imprecisions. Please use them at your own risk! Moreover, your comments are more than welcome! Introduction The first goal of the papers of Bhatt-Morrow-Scholze is to define two cohomology theories which can be used to recover étale , crystalline and de Rham cohomology . This is very interesting from the point of view of
Post a Comment
Read more

TANT 21+22 - What's next?

-
Hello there! These are notes for the last two classes of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . In the latest classes of the course we have struggled with understanding class field theory , which is the study of abelian extensions of a field. More precisely, given a field \( K \) which is either finite, local or global we can define a group \( C_K \) by setting \[ C_K := \begin{cases} \mathbb{Z}, \ \text{if} \ F \ \text{is finite} \\ K^{\times}, \ \text{if} \ F \ \text{is local} \\ \mathbb{I}_K/K^{\times}, \ \text{if} \ F \ \text{is global} \end{cases} \] and class field theory gives us an Artin map \( \theta_K \colon C_K \to G_K^{\text{ab}} \), where \( G_K \) is the absolute Galois group of \( K \). We know moreover that this map has some functoriality property when we change the field \( K \), and that the map \( \widehat{\theta_K} \colon \widehat{C_K} \to G_K^{\text{ab}} \) is a
Post a Comment
Read more

TANT 20 - Class field theory in terms of ideals

-
Hello there! These are notes for the twentieth class of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . In the previous lecture we used the idelic class group \( C_K \) to give the statement of the main theorem of global class field theory. Moreover, we related this group to the "traditional" class group \( \mathfrak{C}_K \) by proving that \[ \mathfrak{C}_K \cong \frac{C_K}{(\widehat{\mathcal{O}_K^{\times}} \cdot \mathbb{I}_{K,\infty}) \cdot K^{\times}}. \] In this lecture we will use this isomorphism to state the main theorem of global class field theory in terms of ideal classes. In order to do so, we need to prove that the groups \( \overline{U}_K^{\mathfrak{m}} \subseteq C_K \) that we defined in the last lecture are of finite index in \( C_K \), which is what we will do in the second section.
Post a Comment
Read more

TANT 19 - Global class field theory

-
Image
Hello there! These are notes for the nineteenth class of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . In the last lecture we defined the ring of adèles \( \mathbb{A}_K \), the group of idèles \( \mathbb{I}_K := \mathbb{A}_K^{\times} \) and the idèle class group \( C_K := \mathbb{I}_K/K^{\times} \) of a global field \( K \). We have moreover seen that we can construct a continuous group homomorphism \( \mathbb{I}_K \to G_K^{\text{ab}} \) by gluing together all the local Artin maps. The biggest deal to complete the proof of the main theorem of global class field theory is then to show that this map is surjective and its kernel contains \( K^{\times} \). Thus, this map induces a global Artin map \( \theta_K \colon C_K \to  G_K^{\text{ab}} \) which in turn induces an isomorphism \( \widehat{C_K} \cong G_K^{\text{ab}} \). This isomorphism will give us a bijective correspondence between open
Post a Comment
Read more

TANT 18 - The ring of adèles

-
Image
Hello there! These are notes for the eighteenth class of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . In the previous lecture we saw that for every local field \( K \) we have a natural isomorphism \( G_K^{\text{ab}} \cong \widehat{K^{\times}} \). This generalizes the isomorphism \( G_{\mathbb{Q}_p}^{\text{ab}} \cong \widehat{\mathbb{Q}_p^{\times}} \) which we proved in the sixteenth lecture as a consequence of the local version of the theorem of Kronecker and Weber. In the same lecture we also proved that \( G_{\mathbb{Q}}^{\text{ab}} \cong \widehat{\mathbb{Z}} \) as a consequence of the global version of the theorem of Kronecker and Weber. Thus it is a natural question to ask if we can generalize this result to an arbitrary number field \( K \). In particular, it would be nice if we could "glue" the local Artin maps \( \theta_{\mathfrak{p}} \colon K_{\mathfrak{p}} \to G_{K_
Post a Comment
Read more

TANT 17 - Local class field theory

-
Image
Hello there! These are notes for the seventeenth class of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . In the previous lecture we proved the global version of the theorem of Kronecker and Weber, and we have also seen how this theorem enables us to compute the abelian part of the absolute Galois group \( G_{\mathbb{Q}} \). It is now natural to ask: can we do so for every number field \( K \)? More precisely, can we find an analogue of roots of unity which would enable us to characterize abelian extensions of a number field \( K \), and thus to compute the group \( G_K^{\text{ab}} \)? It turns out that the second question has a positive answer, whereas the first question is rather hopeless (apart from one specific case, which we will see in the last week of the course). This last part of the course is thus devoted to compute the abelian group \( G_K^{\text{ab}} \) for every number field \
Post a Comment
Read more

TANT 16 - From local to global Kronecker-Weber

-
Image
Hello there! These are notes for the sixteenth class of the course " Topics in algebra and number theory " held in Block 4 of the academic year 2017/18 at the University of Copenhagen . In the previous lecture we have (almost) proved that every finite abelian extension of \( \mathbb{Q}_p \) is contained in a cyclotomic extension. We will use this local result to prove that the same is true for finite abelian extensions of \( \mathbb{Q} \). This is the famous Theorem of Kronecker and Weber , which was completely proved by David Hilbert in his paper " Ein neuer Beweis des Kroneckerschen Fundamentalsatzes über Abelsche Zahlkörper ". Since the theorem is so old you may guess that Hilbert didn't use (as we do) all the machinery of local fields to prove the theorem. Indeed his proof was only based on ramification theory of local fields. If you want to read a modern version of this simple proof, you can read this paper (and the correction to it ) of Marvin J. Gre
Post a Comment
Read more