TANT 19 - Global class field theory
Hello there! These are notes for the nineteenth class of the course "Topics in algebra and number theory" held in Block 4 of the academic year 2017/18 at the University of Copenhagen.
In the last lecture we defined the ring of adèles \( \mathbb{A}_K \), the group of idèles \( \mathbb{I}_K := \mathbb{A}_K^{\times} \) and the idèle class group \( C_K := \mathbb{I}_K/K^{\times} \) of a global field \( K \). We have moreover seen that we can construct a continuous group homomorphism \( \mathbb{I}_K \to G_K^{\text{ab}} \) by gluing together all the local Artin maps. The biggest deal to complete the proof of the main theorem of global class field theory is then to show that this map is surjective and its kernel contains \( K^{\times} \). Thus, this map induces a global Artin map \( \theta_K \colon C_K \to G_K^{\text{ab}} \) which in turn induces an isomorphism \( \widehat{C_K} \cong G_K^{\text{ab}} \).
This isomorphism will give us a bijective correspondence between open subgroups of finite index in \( C_K \) and finite abelian extensions of \( K \). We have seen that we can make this correspondence explicit in local class field theory. Namely, if \( F \) is a local field we have that all the open subgroups of finite index of \( F^{\times} \) are of the form \( \operatorname{N}_{L/F}(L^{\times}) \), for some finite abelian extension \( F \subseteq L \). This gave us the explicit version of local Artin reciprocity thanks to the functoriality property that it satisfies.
We will see that something similar happens in global class field theory: for every finite extension \( K \subseteq L \) we can define a norm \( \operatorname{N}_{L/K} \) on the idèle class group \( C_K \), and we will see that every open subgroup of finite index in \( C_K \) is of the form \( \operatorname{N}_{L/K}(C_L) \) for some finite abelian extension \( K \subseteq L \). This, combined with the functoriality property of the Artin map, will give us the explicit version of global class field theory.
Definition 1 Let \( K \subseteq L \) be a finite extension of global fields. Then we define the norm map \( \operatorname{N}_{L/K} \colon \mathbb{A}_L \to \mathbb{A}_K \) by setting \[ \operatorname{N}_{L/K}((a_w)_{w \in \Sigma_L}) := \left( \prod_{w \mid v} \operatorname{N}_{L_{w}/K_{v}}(a_w) \right)_{v \in \Sigma_K} \]
Observe that this map is well defined. Namely since \( K_v \subseteq L_w \) is a finite extension of complete fields, we have that \( \lvert \cdot \rvert_w \) is equivalent to \( \lvert \operatorname{N}_{L_{w}/K_{v}}(\cdot) \rvert_v \) for every \( x \in L_w \), and this implies that \( \operatorname{N}_{L_{w}/K_{v}}(A_{L_w}) \subseteq A_{K_v} \). Here \( \lvert \cdot \rvert_{v} \) and \( \lvert \cdot \rvert_{w} \) are some absolute values associated to the places \( v \) and \( w \) respectively.
Remark 2 We know that a place \( v \in \Sigma_K \) is an equivalence class of absolute values, and thus determines a topology on \( K \). However, it is not immediately clear from what we already know how one can associate a canonical absolute value to this place. One way to do so is to observe that if \( K \) is a local field (i.e. a topological field whose topology is locally compact and not discrete) then in particular \( (K,+) \) is a locally compact abelian group. It turns out that one can canonically define a measure on the Borel \( \sigma \)-algebra \( \mathcal{B} \) of every such a group. Recall that \( \mathcal{B} \) is the sub-algebra of the power set \( \mathcal{P}(K) \) generated by the open subsets of \( K \), and that a measure on \( \mathcal{B} \) is any function \( \mu \colon \mathcal{B} \to \mathbb{R}_{\geq 0} \cup \{ + \infty \} \) such that \( \mu(\emptyset) = 0 \) and \[ \mu\left( \bigcup_{k = 1}^{+\infty} E_k \right) = \sum_{k = 1}^{+\infty} \mu(E_k) \] for every collection of mutually disjoint subsets \( \{ E_k \} \subseteq \mathcal{B} \). If one asks that \( \mu(x + S) = \mu(S) \) for every \( x \in K \), that \( \mu(C) < +\infty \) for every compact subset \( C \subseteq K \) and that \( \mu \) is inner and outer regular then one gets a Haar measure on the locally compact abelian group \( (K,+) \). André Weil proved that such a measure exists on every locally compact abelian group (see this blog post by Terence Tao), and it is not tough to see that it is uniquely determined up to constant, i.e. if \( \mu, \mu' \) are two Haar measures then \( \mu(x) = \alpha \mu'(x) \) for every \( x \in K \) and for some constant \( \alpha \in \mathbb{R}_{> 0} \) which does not depend on \( x \). Using this fact one can prove that for every local field \( K \) and every measurable set \( S \in \mathcal{B} \) with \( \mu(S) < +\infty \) the map \( \phi_{K} \colon K \to \mathbb{R}_{\geq 0} \) defined by \( \phi(x) := \mu(x \, S)/\mu(S) \) is a well defined absolute value which does not depend on \( S \). Hence for every global field \( F \) and every place \( v \in \Sigma_F \) we have a canonical absolute value \( \lvert \cdot \rvert_v \) induced by the restriction of \( \phi_{F_v} \) to \( F \). In particular if \( v \in \Sigma_K^{\infty} \) corresponds to a prime ideal \( \mathfrak{p} \subseteq \mathcal{O}_F \) then we have that \( \lvert x \rvert_v = (\# \mathcal{O}_F/\mathfrak{p})^{- v_{\mathfrak{p}}(x)} \). Moreover if \( v \in \Sigma_{F,\infty} \) then \( \lvert \cdot \rvert_v \) coincides with the canonical absolute value if \( K_v \cong \mathbb{R} \) and with the square of the canonical absolute value if \( K_v \cong \mathbb{C} \).
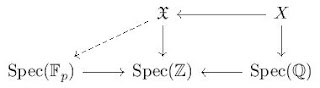
The key property here is that the norm map defined above commutes with the field norm maps. Namely, if \( \operatorname{N}_{L/K} \colon L \to K \) is the canonical norm map and \( K \hookrightarrow \mathbb{A}_K \) is the diagonal inclusion then the diagram on the right commutes. This boils down to prove that for every \( x \in L \) we have that \[ \operatorname{N}_{L/K}(x) = \prod_{w \mid v} \operatorname{N}_{L_w/K_v}(x) \] where we view \( x \in L_w \) under the canonical inclusion \( L \hookrightarrow L_w \). To prove this we only need to observe that if \( v \in \Sigma_K \) is any place then we know from Theorem 4 of the twelfth lecture that\( K_v \otimes_K L \cong \prod_{w \mid v} L_w \). Moreover if \( V_1 \to V_2 \) is a map of finite dimensional vector spaces over a field \( F \) and \( W \) is another finite dimensional vector space, one can easily see that \( \det(V_1 \to V_2) = \det(V_1 \otimes_K W \to V_2 \otimes_K W) \). These two facts imply the formula because \( \operatorname{N}_{L/K}(x) := \det(L \xrightarrow{\cdot x} L) \), and the map induced by \( L \xrightarrow{\cdot x} L \) on \( K_v \otimes_K L \) is indeed \( \prod_{w \mid v} L_w \xrightarrow{\cdot x} L_w \).
This observation implies in particular that we can define a norm map \( \operatorname{N}_{L/K} \colon C_L \to C_K \) by restricting the norm map \( \operatorname{N}_{L/K} \colon \mathbb{A}_L \to \mathbb{A}_K \) to a map \( \operatorname{N}_{L/K} \colon \mathbb{I}_L \to \mathbb{I}_K \) (which we can do because this norm is clearly multiplicative, and thus sends units to units), and then we can use what we have just seen to obtain the desired map from \( C_L := \mathbb{I}_L/L^{\times} \) to \( C_K := \mathbb{I}_K/K^{\times} \).
We can now enounce the main theorem of global class field theory.
Theorem 3 Let \( K \) be a global field and let \( \mathbb{I}_K \) be the group of adèles associated to \( K \). Then the map \( \mathbb{I}_K \to G_K^{\text{ab}} \) obtained by gluing together all the local Artin maps (see the previous lecture) is trivial on \( K^{\times} \). Thus it induces a global Artin map \( \theta_K \colon C_K \to G_K^{\text{ab}} \), where \( C_K := \mathbb{I}_K/K^{\times} \). The map \( \theta_K \) is a continuous group homomorphism with the following properties:
Theorem 4 Let \( K \) be a global field. Then every subgroup of \( C_K \) of finite index is equal to \( \operatorname{N}_{L/K}(C_L) \) for a unique finite extension \( K \subseteq L \).
Again as before, we get as a corollary that if \( K \subseteq L \) is a finite abelian extension of global fields we have an isomorphism \( \operatorname{Gal}(L/K) \cong C_K/(\operatorname{N}_{L/K}(L^{\times})) \).
Observe finally that the norm on the adèle commutes also with the norm on the local fields, at least when restricted to the idèle group. Namely, if \( K \) is a global field and \( v \in \Sigma_K \) we have an embedding of topological groups \begin{align} K_v^{\times} &\hookrightarrow \mathbb{I}_K \\ x &\mapsto (1,1,\dots,1,\underbrace{x}_{\text{at place} \ v},1,\dots) \end{align} and these embeddings clearly make the diagram on the right commutative.
Thus the functoriality of the local and global Artin maps, and the compatibility between the two of them are expressed in the following monstrous commutative cube:
In the last lecture we defined the ring of adèles \( \mathbb{A}_K \), the group of idèles \( \mathbb{I}_K := \mathbb{A}_K^{\times} \) and the idèle class group \( C_K := \mathbb{I}_K/K^{\times} \) of a global field \( K \). We have moreover seen that we can construct a continuous group homomorphism \( \mathbb{I}_K \to G_K^{\text{ab}} \) by gluing together all the local Artin maps. The biggest deal to complete the proof of the main theorem of global class field theory is then to show that this map is surjective and its kernel contains \( K^{\times} \). Thus, this map induces a global Artin map \( \theta_K \colon C_K \to G_K^{\text{ab}} \) which in turn induces an isomorphism \( \widehat{C_K} \cong G_K^{\text{ab}} \).
This isomorphism will give us a bijective correspondence between open subgroups of finite index in \( C_K \) and finite abelian extensions of \( K \). We have seen that we can make this correspondence explicit in local class field theory. Namely, if \( F \) is a local field we have that all the open subgroups of finite index of \( F^{\times} \) are of the form \( \operatorname{N}_{L/F}(L^{\times}) \), for some finite abelian extension \( F \subseteq L \). This gave us the explicit version of local Artin reciprocity thanks to the functoriality property that it satisfies.
We will see that something similar happens in global class field theory: for every finite extension \( K \subseteq L \) we can define a norm \( \operatorname{N}_{L/K} \) on the idèle class group \( C_K \), and we will see that every open subgroup of finite index in \( C_K \) is of the form \( \operatorname{N}_{L/K}(C_L) \) for some finite abelian extension \( K \subseteq L \). This, combined with the functoriality property of the Artin map, will give us the explicit version of global class field theory.
The main statement of global class field theory
As we have defined the global Artin map \( \theta_K \) by gluing together the local ones, it is natural to expect that the "norm map" \( \operatorname{N}_{L/K} \colon C_L \to C_K \) will also be defined by a similar gluing operation. And this is precisely what happens.Definition 1 Let \( K \subseteq L \) be a finite extension of global fields. Then we define the norm map \( \operatorname{N}_{L/K} \colon \mathbb{A}_L \to \mathbb{A}_K \) by setting \[ \operatorname{N}_{L/K}((a_w)_{w \in \Sigma_L}) := \left( \prod_{w \mid v} \operatorname{N}_{L_{w}/K_{v}}(a_w) \right)_{v \in \Sigma_K} \]
Observe that this map is well defined. Namely since \( K_v \subseteq L_w \) is a finite extension of complete fields, we have that \( \lvert \cdot \rvert_w \) is equivalent to \( \lvert \operatorname{N}_{L_{w}/K_{v}}(\cdot) \rvert_v \) for every \( x \in L_w \), and this implies that \( \operatorname{N}_{L_{w}/K_{v}}(A_{L_w}) \subseteq A_{K_v} \). Here \( \lvert \cdot \rvert_{v} \) and \( \lvert \cdot \rvert_{w} \) are some absolute values associated to the places \( v \) and \( w \) respectively.
Remark 2 We know that a place \( v \in \Sigma_K \) is an equivalence class of absolute values, and thus determines a topology on \( K \). However, it is not immediately clear from what we already know how one can associate a canonical absolute value to this place. One way to do so is to observe that if \( K \) is a local field (i.e. a topological field whose topology is locally compact and not discrete) then in particular \( (K,+) \) is a locally compact abelian group. It turns out that one can canonically define a measure on the Borel \( \sigma \)-algebra \( \mathcal{B} \) of every such a group. Recall that \( \mathcal{B} \) is the sub-algebra of the power set \( \mathcal{P}(K) \) generated by the open subsets of \( K \), and that a measure on \( \mathcal{B} \) is any function \( \mu \colon \mathcal{B} \to \mathbb{R}_{\geq 0} \cup \{ + \infty \} \) such that \( \mu(\emptyset) = 0 \) and \[ \mu\left( \bigcup_{k = 1}^{+\infty} E_k \right) = \sum_{k = 1}^{+\infty} \mu(E_k) \] for every collection of mutually disjoint subsets \( \{ E_k \} \subseteq \mathcal{B} \). If one asks that \( \mu(x + S) = \mu(S) \) for every \( x \in K \), that \( \mu(C) < +\infty \) for every compact subset \( C \subseteq K \) and that \( \mu \) is inner and outer regular then one gets a Haar measure on the locally compact abelian group \( (K,+) \). André Weil proved that such a measure exists on every locally compact abelian group (see this blog post by Terence Tao), and it is not tough to see that it is uniquely determined up to constant, i.e. if \( \mu, \mu' \) are two Haar measures then \( \mu(x) = \alpha \mu'(x) \) for every \( x \in K \) and for some constant \( \alpha \in \mathbb{R}_{> 0} \) which does not depend on \( x \). Using this fact one can prove that for every local field \( K \) and every measurable set \( S \in \mathcal{B} \) with \( \mu(S) < +\infty \) the map \( \phi_{K} \colon K \to \mathbb{R}_{\geq 0} \) defined by \( \phi(x) := \mu(x \, S)/\mu(S) \) is a well defined absolute value which does not depend on \( S \). Hence for every global field \( F \) and every place \( v \in \Sigma_F \) we have a canonical absolute value \( \lvert \cdot \rvert_v \) induced by the restriction of \( \phi_{F_v} \) to \( F \). In particular if \( v \in \Sigma_K^{\infty} \) corresponds to a prime ideal \( \mathfrak{p} \subseteq \mathcal{O}_F \) then we have that \( \lvert x \rvert_v = (\# \mathcal{O}_F/\mathfrak{p})^{- v_{\mathfrak{p}}(x)} \). Moreover if \( v \in \Sigma_{F,\infty} \) then \( \lvert \cdot \rvert_v \) coincides with the canonical absolute value if \( K_v \cong \mathbb{R} \) and with the square of the canonical absolute value if \( K_v \cong \mathbb{C} \).
The key property here is that the norm map defined above commutes with the field norm maps. Namely, if \( \operatorname{N}_{L/K} \colon L \to K \) is the canonical norm map and \( K \hookrightarrow \mathbb{A}_K \) is the diagonal inclusion then the diagram on the right commutes. This boils down to prove that for every \( x \in L \) we have that \[ \operatorname{N}_{L/K}(x) = \prod_{w \mid v} \operatorname{N}_{L_w/K_v}(x) \] where we view \( x \in L_w \) under the canonical inclusion \( L \hookrightarrow L_w \). To prove this we only need to observe that if \( v \in \Sigma_K \) is any place then we know from Theorem 4 of the twelfth lecture that\( K_v \otimes_K L \cong \prod_{w \mid v} L_w \). Moreover if \( V_1 \to V_2 \) is a map of finite dimensional vector spaces over a field \( F \) and \( W \) is another finite dimensional vector space, one can easily see that \( \det(V_1 \to V_2) = \det(V_1 \otimes_K W \to V_2 \otimes_K W) \). These two facts imply the formula because \( \operatorname{N}_{L/K}(x) := \det(L \xrightarrow{\cdot x} L) \), and the map induced by \( L \xrightarrow{\cdot x} L \) on \( K_v \otimes_K L \) is indeed \( \prod_{w \mid v} L_w \xrightarrow{\cdot x} L_w \).
This observation implies in particular that we can define a norm map \( \operatorname{N}_{L/K} \colon C_L \to C_K \) by restricting the norm map \( \operatorname{N}_{L/K} \colon \mathbb{A}_L \to \mathbb{A}_K \) to a map \( \operatorname{N}_{L/K} \colon \mathbb{I}_L \to \mathbb{I}_K \) (which we can do because this norm is clearly multiplicative, and thus sends units to units), and then we can use what we have just seen to obtain the desired map from \( C_L := \mathbb{I}_L/L^{\times} \) to \( C_K := \mathbb{I}_K/K^{\times} \).
We can now enounce the main theorem of global class field theory.
Theorem 3 Let \( K \) be a global field and let \( \mathbb{I}_K \) be the group of adèles associated to \( K \). Then the map \( \mathbb{I}_K \to G_K^{\text{ab}} \) obtained by gluing together all the local Artin maps (see the previous lecture) is trivial on \( K^{\times} \). Thus it induces a global Artin map \( \theta_K \colon C_K \to G_K^{\text{ab}} \), where \( C_K := \mathbb{I}_K/K^{\times} \). The map \( \theta_K \) is a continuous group homomorphism with the following properties:
- if \( K \) is a number field then \( \theta \) is surjective and its kernel is the connected component of \( C_K \) containing the identity;
- if \( K \) is the function field of a curve defined over \( \mathbb{F}_q \) then \( \theta \) is injective and its image coincides with those maps \( \sigma \colon K^{\text{ab}} \to K^{\text{ab}} \) which restricted to \( \mathbb{F}_q^{\text{ab}} \) are equal to an integral power of the topological generator of \( G_{\mathbb{F}_q}^{\text{ab}} = G_{\mathbb{F}_q} \cong \widehat{Z} \).
- for every finite extension of global fields \( K \subseteq L \) the square on the right is commutative;
- the map \( \theta_K \) induces an isomorphism \( \widehat{C_K} \cong G_K^{\text{ab}} \);
Theorem 4 Let \( K \) be a global field. Then every subgroup of \( C_K \) of finite index is equal to \( \operatorname{N}_{L/K}(C_L) \) for a unique finite extension \( K \subseteq L \).
Again as before, we get as a corollary that if \( K \subseteq L \) is a finite abelian extension of global fields we have an isomorphism \( \operatorname{Gal}(L/K) \cong C_K/(\operatorname{N}_{L/K}(L^{\times})) \).
Observe finally that the norm on the adèle commutes also with the norm on the local fields, at least when restricted to the idèle group. Namely, if \( K \) is a global field and \( v \in \Sigma_K \) we have an embedding of topological groups \begin{align} K_v^{\times} &\hookrightarrow \mathbb{I}_K \\ x &\mapsto (1,1,\dots,1,\underbrace{x}_{\text{at place} \ v},1,\dots) \end{align} and these embeddings clearly make the diagram on the right commutative.Thus the functoriality of the local and global Artin maps, and the compatibility between the two of them are expressed in the following monstrous commutative cube:
Moduli and ray class fields
The theorem of Kronecker and Weber allows us to embed every abelian number field (i.e. a number field which is Galois over \( \mathbb{Q} \) with abelian Galois group) inside a cyclotomic field. In particular, every cyclotomic field is obtained by adjoining to \( \mathbb{Q} \) a root of unity \( \zeta_n \), i.e. the value at an integer point of the analytic function \( f(z) \colon \mathbb{C}^{\times} \to \mathbb{C}^{\times} \) defined as \( f(z) := e^{2 \pi i/z} \). There is also a similar result in positive characteristic, concerning finite abelian extensions of the field \( \mathbb{F}_p(T) \) (see this paper by Julio Cesar Salas-Torres, Martha Rzedowski-Calderón and Gabriel Villa-Salvador).
For a general global field \( K \) we have now a description of the group \( G_K^{\text{ab}} \) and we will use it to define an analogue of cyclotomic fields for \( K \). In order to do so, we need the following definition.
Definition 5 Let \( K \) be a field. A modulus for \( K \) is a map \( \mathfrak{m} \colon \Sigma_K \to \mathbb{N} \) which has finite support (i.e. \( \mathfrak{m}(v) = 0 \) for all but a finite number of places of \( K \)) and such that for every infinite place \( v \in \Sigma_{K,\infty} \) we have that \( \mathfrak{m}(v) = 0 \) if \( K_v \cong \mathbb{C} \) and \( \mathfrak{m}(v) \in \{0, 1\} \) if \( K_v \cong \mathbb{R} \).
For every modulus \( \mathfrak{m} \) of a global field, and for every place \( v \in \Sigma_K \) we can now define groups \( U_K^{\mathfrak{m}}(v) \subseteq A_{K_v}^{\times} \) by setting \[ U_K^{\mathfrak{m}}(v) := \begin{cases} A_{K_v}^{\times}, \ \text{if} \ \mathfrak{m}(v) = 0 \\ \mathbb{R}_{> 0}, \ \text{if} \ \mathfrak{m}(v) = 1 \ \text{and} \ K_v \cong \mathbb{R} \\ 1 + \mathfrak{m}_{K_v}^{\mathfrak{m}(v)}, \ \text{if} \ \mathfrak{m}(v) = 1 \ \text{and} \ v \in \Sigma_K^{\infty} \end{cases} \] and we set \( U_K^{\mathfrak{m}} := \prod_{v \in \Sigma_K} U_K^{\mathfrak{m}}(v) \subseteq \mathbb{I}_K \).
It is not difficult to see that the groups \( \{ U_K^{\mathfrak{m}} \}_{\mathfrak{m}} \) form a system of open neighbourhoods of the identity in \( \mathbb{I}_K \). What is tougher to prove is that the images of these groups in the quotient \( C_K := \mathbb{I}_K/K^{\times} \) are subgroups of finite index. This follows from the finiteness of the class group of global fields, as we will see in the next section and in the next lecture. Nevertheless, using this we can give the following definition.
Definition 6 Let \( K \) be a field and \( \mathfrak{m} \) be a modulus for \( K \). We define the ray class field \( K(\mathfrak{m}) \supseteq K \) as the unique finite abelian extension such that \( \operatorname{N}_{K(\mathfrak{m})/K}((K(\mathfrak{m}))^{\times}) = \overline{U}_K^{\mathfrak{m}} \).
Definition 7 The ray class field corresponding to the trivial modulus \( \mathfrak{m}(v) = 0 \) for all \( v \in \Sigma_K \) is called the Hilbert class field of the number field \( K \). The ray class field corresponding to the modulus defined by \[ \mathfrak{m}(v) = \begin{cases} 1, \ \text{if} \ K_v \cong \mathbb{R} \\ 0, \ \text{otherwise} \end{cases} \] is called the narrow class field of \( K \).
Using the properties of the global Artin map, and what we have seen on unramified extensions in the previous lecture, we see that the extension \( K \subseteq K({\mathfrak{m}}) \) is unramified at every place \( v \in \Sigma_K \) such that \( \mathfrak{m}(v) = 0 \). In particular, the Hilbert class field of \( K \) is the maximal abelian extension of \( K \) which is unramified at all places, and the narrow class field is the maximal abelian extension which is unramified at all finite places.
Since \( \{ \overline{U}_K^{\mathfrak{m}} \} \) form a system of open neighborhoods of the identity of \( C_K \) we have also that every finite abelian extension \( K \subseteq L \) is contained in a ray class field \( K(\mathfrak{m}) \). Thus, ray class fields play for \( K \) the same role that the cyclotomic fields play for \( \mathbb{Q} \). Actually, we will see in the next lecture that the ray class fields for \( \mathbb{Q} \) are precisely the cyclotomic fields.
It would be nice if we could find a function \( f_K \) which associated to every modulus \( \mathfrak{m} \) an algebraic number such that \( K^{\mathfrak{m}} = K(f_K(\mathfrak{m})) \), as it happens over \( \mathbb{Q} \). This is known as "Hilbert's 12th problem" and seems to be out of reach for most number fields, but can be done for imaginary quadratic fields \( K = \mathbb{Q}(\sqrt{-d}) \), using modular forms and elliptic curves (see Chapter II of the book "Advanced topics in the arithmetic of elliptic curves" by Joseph H. Silverman).
Idèles and ideals
We have just seen how the functoriality of the Artin map relatively to a finite extension of global fields \( K \subseteq L \) can be expressed using a norm map on the idelic class group, defined by gluing together all the norm maps associated to all the possible completions of the fields \( K \) and \( L \). There are also a couple of other maps defined on the group \( C_K \) which will help us to relate the idelic class group to the (standard) class group \( \mathfrak{Cl}(K) \) of the field \( K \), and thus to rephrase the main theorem of global class field theory in terms of prime ideals of \( \mathcal{O}_K \).
Remark 8 Recall that, if \( K \) is a global field, we define \( \mathcal{O}_K \) to be the integral closure of \( \mathbb{Z} \) (if \( K \) is a number field) or \( \mathbb{F}_q[x] \) (if \( K \) is a function field over \( \mathbb{F}_q \)) inside \( K \). Moreover, a fractional ideal is an \( \mathcal{O}_K \) sub-module of \( K \) which is finitely generated, and we denote by \( \mathcal{I}_K \) the ideal group of \( K \), i.e. the group of all the fractional ideals with the product operation. Since \( \mathcal{O}_K \) is a Dedekind domain we have that \( \mathcal{I}_K \cong \mathbb{Z}^{\Sigma_{K}^{\infty}} \), i.e. the group of fractional ideals is isomorphic to the free abelian group on the set of all non-Archimedean places of \( K \).
Finally, we define the class group \( \mathfrak{C}_K \) as the quotient of \( \mathcal{I}_K \) by the subgroup of all principal ideals \( \mathcal{P}_K := \{ x \mathcal{O}_K \mid x \in K \} \).
Historically, the group of idèles \( \mathbb{I}_K \) was defined to be a generalization of the group of ideals \( \mathcal{I}_K \). Thus we now understand why \( C_K \) is called "idelic class group": it is the quotient of the group of idèles by the "principal idèles" \( K^{\times} \hookrightarrow \mathbb{I}_K \).
There is a simple way to relate the group \( \mathbb{I}_K \) to \( \mathcal{I}_K \). Indeed, we can define a map \begin{align} \varphi \colon \mathbb{I}_K &\to \mathcal{I}_K \\ (\alpha_v)_{v \in \Sigma_K} &\mapsto \prod_{v \in \Sigma_K^{\infty}} \mathfrak{p}_v^{v(\alpha_v)} \end{align} where \( \mathfrak{p}_v \subseteq \mathcal{O}_K \) is the unique prime ideal associated to \( v \) by Ostrowski's theorem.
This map is clearly surjective because we can write every fractional ideal \( \mathfrak{a} \in \mathcal{I}_K \) as \( \mathfrak{a} = \mathfrak{p}_1^{m_1} \cdots \mathfrak{p}_n^{m_n} \) for some prime ideals \( \mathfrak{p}_1,\dots,\mathfrak{p}_n \subseteq \mathcal{O}_K \) and some \( m_1,\dots,m_n \in \mathbb{Z} \). Let \( S = \{ v_1,\dots,v_n \} \) be the finite set of places corresponding to \( \mathfrak{p}_1,\dots,\mathfrak{p}_n \), and observe that \( \mathfrak{a} = \varphi((a_v)) \) where \( a_v = 1 \) if \( v \notin S \) and \( a_{v_j} = m_j \) for all \( j \in \{1,\dots,n\} \).
Observe now that \( \varphi \) sends principal idèles to principal ideals. Namely, for every \( \alpha \in K^{\times} \) we have the decomposition \[ \alpha \mathcal{O}_K = \prod_{v \in \Sigma_K^{\infty}} \mathfrak{p}_v^{v(\alpha)} = \varphi(\iota(\alpha)) \] where \( \iota \colon K^{\times} \hookrightarrow \mathbb{I}_K \) is the diagonal embedding.
This shows that we get a surjective map \( \widetilde{\varphi} \colon C_K \twoheadrightarrow \mathfrak{C}_K \) which fits in the following diagram
where every row and column is exact, and the map \( K^{\times} \twoheadrightarrow \mathcal{P}_K \) sends \( \alpha \in K^{\times} \) to \( \alpha \cdot \mathcal{O}_K \). To prove this we need to prove that \( \ker(\varphi) = \widehat{ \mathcal{O}_K^{\times} } \cdot \mathbb{I}_{K,\infty} \). Indeed recall that the unity in \( \mathcal{I}_K \) is \( \mathcal{O}_K \), and thus \( (a_v)_{v \in \Sigma_K} \in \ker(\varphi) \) if and only if \( \varphi((a_v)) = \prod_{v \in \Sigma_K^{\infty}} \mathfrak{p}_v^{v(a_v)} = \mathcal{O}_K \), which is true if and only if \( v(a_v) = 0 \) for all \( v \in \Sigma_K^{\infty} \), which is finally true precisely when \( (a_v) \in \widehat{\mathcal{O}_K^{\times}} \cdot \mathbb{I}_{K,\infty} \). Thus the horizontal and vertical sequences in the diagram above are indeed exact and we have that \[ \mathfrak{C}_K \cong \frac{C_K}{\pi(\widehat{\mathcal{O}_K^{\times}} \cdot \mathbb{I}_{K,\infty})} \] where \( \pi \colon \mathbb{I}_K \twoheadrightarrow C_K \) is the quotient map. This gives us a relation between the idelic class group and the class group of a field which will allow us to restate the main theorem of global class field theory in terms of ideals in the next lecture.
Conclusions and references
In this lecture we managed to:
- give the statement of the main theorem of global class field theory;
- define ray class fields as analogues of cyclotomic extensions for general global fields;
- relate the idelic class group to the "classical" class group of a global field.
- these notes by Andrew Sutherland;
- this summary by Bjorn Poonen;
- Sections V.4 and V.5 of the notes "Class field theory" by James S. Milne;
- Sections III.6 and III.7 of the book "Class field theory - The Bonn Lectures" by Jürgen Neukirch.
Comments
Post a Comment