TANT 17 - Local class field theory
Hello there! These are notes for the seventeenth class of the course "Topics in algebra and number theory" held in Block 4 of the academic year 2017/18 at the University of Copenhagen.
In the previous lecture we proved the global version of the theorem of Kronecker and Weber, and we have also seen how this theorem enables us to compute the abelian part of the absolute Galois group \( G_{\mathbb{Q}} \). It is now natural to ask: can we do so for every number field \( K \)? More precisely, can we find an analogue of roots of unity which would enable us to characterize abelian extensions of a number field \( K \), and thus to compute the group \( G_K^{\text{ab}} \)?
It turns out that the second question has a positive answer, whereas the first question is rather hopeless (apart from one specific case, which we will see in the last week of the course). This last part of the course is thus devoted to compute the abelian group \( G_K^{\text{ab}} \) for every number field \( K \). This study is called "class field theory" and, as we will see later on, has its foundations in the laws of quadratic and cubic reciprocity envisioned by Gauß.
As we did for \( \mathbb{Q} \) we will look first of all at the local world and then patch together all the information that we have there to get a global statement. In order to do this last step we will need a new object, the ring of adèles associated to a number field, which we will study for the next few lectures.
\begin{aligned}
G \times G &\to G \\
(g,h) &\mapsto g h
\end{aligned}
\qquad \text{and} \qquad
\begin{aligned}
G &\to G \\ g &\mapsto g^{-1}
\end{aligned} \] are continuous. Profinite groups are a particular type of topological groups.
Definition 1 A topological group \( G \) is called profinite if it is also a Stone space, i.e. Hausdorff, compact and totally disconnected.
It turns out that there is a canonical way to associate a profinite group to any topological group.
Definition 2 Let \( G \) be a topological group. We define its profinite completion as the topological group \[ \widehat{G} := \varprojlim_{\substack{H \trianglelefteq G \\ [G \colon H] < +\infty}} \frac{G}{H} \] where \( H \) runs over all open, normal subgroups of finite index in \( G \). Thus, every finite factor of the inverse limit is endowed with the discrete topology.
The term "pro-finite" makes one think that such a topological group would always be a "limit" of finite groups. Which is precisely what happens.
Theorem 3 Let \( G \) be a topological group. Then \( G \) is profinite if and only if \( G \cong \varprojlim_{i \in I} G_i \), where \( \{ G_i \}_{i \in I} \) is an inverse system of finite, discrete groups.
Proof Observe first of all that \( \varprojlim_{i \in I} G_i \) is a closed subspace of the product \( \prod_{i \in I} G_i \). Indeed the inverse limit is defined as the set of sequences \( (a_i) \in \prod_{i \in I} G_i \) such that for every map \( \phi_{i,j} \colon G_i \to G_j \) of the inverse system we have that \( \phi_{i,j}(a_i) = a_j \). Hence \( \varprojlim_{i \in I} G_i \) is the intersection of the subspaces of \( \prod_{i \in I} G_i \) obtained as \( (\varphi_{i,j})^{-1}(\Delta_j) \) where \[ \varphi_{i,j} \colon \prod_{k \in I} G_k \twoheadrightarrow G_i \times G_j \xrightarrow{\phi_{i,j} \times \operatorname{Id}} G_j \times G_j \] and \( \Delta_j \subseteq G_j \times G_j \) is the diagonal. Observe now that every finite, discrete group \( G_i \) is trivially a Stone space. This implies that \( \varprojlim_{i \in I} G_i \) is a closed subset of a product of Stone spaces, and thus it is a Stone space itself. This follows from the fact that the product of Hausdorff spaces is Hausdorff (see this question on Math StackExchange), the product of compact spaces is compact (by Tychonoff's theorem) and the product of totally disconnected spaces is totally disconnected (see this question on Math StackExchange), and the fact that all these properties are preserved by closed sub-spaces. This shows that \( \varprojlim_{i \in I} G_i \) is profinite, and thus that \( G \) is profinite if it is an inverse limit of finite, discrete groups.
Vice versa, suppose that \( G \) is profinite. Observe that we have a continuous group homomorphism \( G \to \widehat{G} \) given by sending each element \( g \in G \) to the "constant sequence" \( (\pi_H(g))_H \in \widehat{G} \), where \( \pi_H \colon G \to G/H \) is the quotient map. We would like to prove that this continuous map is a homeomorphism, and since both \( G \) and \( \widehat{G} \) are compact and Hausdorff it is sufficient to show that this map is bijective (see Lemma B6.7 of these notes by Tom Leinster). First of all, we prove surjectivity. Let \( \{ g_H \}_H \subseteq G \) be a sequence of elements indexed on the finite-index, normal subgroups of \( G \) such that \( (\pi_H(g_H))_H \in \widehat{G} \). Then by Exercise 4 the cosets \( g_H H \subseteq G \) are all non-empty closed subsets, and for every two finite-index, normal subgroups \( H,K \trianglelefteq G \) we have that \( g_H H \cap g_K K \supseteq g_{H \cap K} (H \cap K) \). This implies that \( \bigcap_H g_H H \neq \emptyset \), by Cantor's intersection theorem. To conclude it is sufficient to observe that for every \( g \in \bigcap_H g_H H \) we have that \( \overline{g} = \pi_H(g_H) \) for all normal subgroups of finite index \( H \trianglelefteq G \). This proves indeed that the image of \( g \) under the map \( G \to \widehat{G} \) is equal to \( (\pi_H(g_H))_H \), and thus that the map is surjective.
To conclude, we want to prove injectivity. Observe that \( (\pi_H(g))_H = 1 \) in \( \widehat{G} \) if and only if \( g \in \bigcap_H H \). Thus to conclude we have to prove that \( \bigcap_H H = \{ 1 \} \). The proof of this result is rather technical, and we will omit it from these notes. If you are interested you can read Lemma 3.9 of these notes by Brian Osserman. Q.E.D.
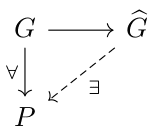
The previous theorem tells us in particular that for every map of topological groups \( G \to P \), where \( P \) is profinite, there exists a unique map of topological groups \( \widehat{G} \to P \) such that the triangle on the right commutes (this is the universal property of the profinite completion).
Exercise 4 Let \( G \) be a topological group, and \( H \leq G \) be a subgroup. Prove that if \( H \) is open then \( H \) is also closed. Moreover, prove that if \( G \) is compact then \( H \) is open if and only if it is closed and has finite index.
The previous theorem tells us that a topological group is "pro-finite" if and only if it is the (inverse) limit of a system of finite groups considered with the discrete topology.
Example 5 Let \( K \subseteq L \) be a Galois extension of field. We have already seen that \( L \) is the direct limit of all the sub-extensions \( K \subseteq M \subseteq L \) such that \( K \subseteq M \) is finite. From this we get that \[ \operatorname{Gal}(L/K) \cong \varprojlim_{\substack{K \subseteq M \subseteq L \\ [M \colon K] < \infty}} \operatorname{Gal}(M/K) \] which implies that the group \( \operatorname{Gal}(L/K) \) is a profinite topological group.
Remark 6 Observe that taking only open normal subgroups of finite index in the definition of completion is necessary. Equivalently, we cannot expect that a profinite group is isomorphic to the profinite completion of itself regarded with the discrete topology. For example in the absolute Galois group \( G_{\mathbb{Q}} \) there are an infinite number of non-open normal subgroups of finite index (see Proposition 7.26 of these notes by James S. Milne). Thanks to a deep theorem of Nikolay Nikolov and Dan Segal (see their papers on this here and here) this implies that \( G_{\mathbb{Q}} \) is not topologically finitely generated, i.e. it is not the closure of a finitely generated subgroup (see also this question on MathOverflow, where the term "profinite completion" does not require the subgroups in the inverse limit to be open).
The main result of local class field theory is that this is true for every local field (see Definition 12 of the ninth lecture).
Theorem 7 Let \( K \) be a local field. Then there exists a unique surjective homomorphism of topological groups \( \theta \colon K^{\times} \to G_K^{\text{ab}} \) (called local Artin map) such that:
This theorem can be proved in many ways: using the Brauer group of a field (as Helmut Hasse did), using Galois cohomology (as Emil Artin did), using formal groups (as Jonathan Lubin and John Tate did) or using explicit approaches (as Jürgen Neukirch and Michael Hazewinkel did). For now, we will only content ourselves with drawing some consequences from this theorem and proving the last part.
Observe first of all that if \( K \subseteq L \) is a finite abelian extension we have a surjective map \[ K^{\times} \xrightarrow{\theta} G_K^{\text{ab}} \twoheadrightarrow \operatorname{Gal}(L/K) \] whose kernel coincides with \( \operatorname{N}_{L/K}(L^{\times}) \subseteq K^{\times} \). Indeed observe that \( L \subseteq K^{\text{ab}} \), which implies, by Galois theory, that \( G_L^{\text{ab}} = \operatorname{Gal}(K^{\text{ab}}/L) \). Thus we get an exact sequence \[ \{1\} \to G_L^{\text{ab}} \to G_K^{\text{ab}} \to \operatorname{Gal}(L/K) \to \{ 1 \} \] where the first map is precisely the restriction map described in the second point of the theorem. Thus using the commutativity of the diagram above and the fact that \( \theta \) is surjective we get that for every element \( x \in K^{\times} \) the automorphism \( \theta(x) \in G_K^{\text{ab}} \) becomes trivial in \( \operatorname{Gal}(L/K) \) if and only if \( x \in \operatorname{N}_{L/K}(L^{\times}) \).
Nevertheless, we can apply the universal property of the profinite completion to get a map \( \widehat{\theta} \colon \widehat{K^{\times}} \to G_K^{\text{ab}} \), and we could hope that this map is an isomorphism. Since the Artin map is already continuous and surjective, we only need to prove that \( \widehat{\theta} \) is injective.
This is equivalent to show that every open, normal subgroup of \( K^{\times} \) of finite index corresponds to an open, normal subgroup of \( G_K^{\text{ab}} \) of finite index. Galois theory tells us that these subgroups correspond to finite abelian extensions \( K \subseteq L \), and in turn we have seen in the previous paragraph that \( \theta^{-1}(\operatorname{Gal}(K^{\text{ab}}/L)) = \operatorname{N}_{L/K}(L^{\times}) \). Thus, proving that \( \widehat{\theta} \) is injective is equivalent to prove the following theorem.
Theorem 8 Let \( K \) be a local field. For every open normal subgroup of finite index \( U \trianglelefteq K^{\times} \) there exists a unique finite abelian extension \( K \subseteq L \) such that \( U = \operatorname{N}_{L/K}(L^{\times}) \).
Proof The uniqueness part is clear using Theorem 7 and Galois theory. If \( K \) is Archimedean, the statement is easy to prove (see Exercise 9 and Exercise 10), thus we will from now on assume that \( K \) is non-Archimedean. In this case, the proof of the existence part of the theorem uses the following facts:
Actually, we have that \( I \supseteq \operatorname{N}_{L/K}(L^{\times}) \cap (A_K^{\times} \cdot (\operatorname{N}_{L/K}(L^{\times}) \cap I)) \) because if \( a \in \operatorname{N}_{L/K}(L^{\times}) \cap (A_K^{\times} \cdot (\operatorname{N}_{L/K}(L^{\times}) \cap I)) \) then we can write \( a = b \, c \) with \( b \in A_K^{\times} \) and \( c \in \operatorname{N}_{L/K}(L^{\times}) \cap I \), which implies that \( b = a c^{-1} \in \operatorname{N}_{L/K}(L^{\times}) \) and thus that \( a \in \operatorname{N}_{L/K}(L^{\times}) \cap A_K^{\times} \subseteq I \).
Since \( A_K^{\times} \cdot (\operatorname{N}_{L/K}(L^{\times}) \cap I) \) contains \( A_K^{\times} \) we can use the second fact to find a finite abelian extension \( K \subseteq E \) such that \( \operatorname{N}_{E/K}(E^{\times}) = A_K^{\times} \cdot (\operatorname{N}_{L/K}(L^{\times}) \cap I) \subseteq I \). Thus we can use Galois theory and the fact that \( \operatorname{Gal}(E/K) \cong K^{\times}/\operatorname{N}_{E/K}(E^{\times}) \) from Theorem 7 to find an intermediate extension \( K \subseteq F \subseteq E \) such that \( I = \operatorname{N}_{F/K}(F^{\times}) \), which is what we wanted to prove. Q.E.D.
Exercise 9 Prove that \( \mathbb{C}^{\times} \) has no non-trivial open subgroups. (Hint: use Exercise 4).
Exercise 10 Prove that the only non-trivial open subgroup of \( \mathbb{R}^{\times} \) is \( \mathbb{R}_{> 0} \). (Hint: use again Exercise 4).
In the previous lecture we proved the global version of the theorem of Kronecker and Weber, and we have also seen how this theorem enables us to compute the abelian part of the absolute Galois group \( G_{\mathbb{Q}} \). It is now natural to ask: can we do so for every number field \( K \)? More precisely, can we find an analogue of roots of unity which would enable us to characterize abelian extensions of a number field \( K \), and thus to compute the group \( G_K^{\text{ab}} \)?
It turns out that the second question has a positive answer, whereas the first question is rather hopeless (apart from one specific case, which we will see in the last week of the course). This last part of the course is thus devoted to compute the abelian group \( G_K^{\text{ab}} \) for every number field \( K \). This study is called "class field theory" and, as we will see later on, has its foundations in the laws of quadratic and cubic reciprocity envisioned by Gauß.
As we did for \( \mathbb{Q} \) we will look first of all at the local world and then patch together all the information that we have there to get a global statement. In order to do this last step we will need a new object, the ring of adèles associated to a number field, which we will study for the next few lectures.
Profinite groups
Before we go on, we need a little introduction to profinite groups, since many of the groups that we will encounter in these lectures will be profinite. Recall that a topological group is a group \( G \) which is also a topological space such that the maps \[\begin{aligned}
G \times G &\to G \\
(g,h) &\mapsto g h
\end{aligned}
\qquad \text{and} \qquad
\begin{aligned}
G &\to G \\ g &\mapsto g^{-1}
\end{aligned} \] are continuous. Profinite groups are a particular type of topological groups.
Definition 1 A topological group \( G \) is called profinite if it is also a Stone space, i.e. Hausdorff, compact and totally disconnected.
It turns out that there is a canonical way to associate a profinite group to any topological group.
Definition 2 Let \( G \) be a topological group. We define its profinite completion as the topological group \[ \widehat{G} := \varprojlim_{\substack{H \trianglelefteq G \\ [G \colon H] < +\infty}} \frac{G}{H} \] where \( H \) runs over all open, normal subgroups of finite index in \( G \). Thus, every finite factor of the inverse limit is endowed with the discrete topology.
The term "pro-finite" makes one think that such a topological group would always be a "limit" of finite groups. Which is precisely what happens.
Theorem 3 Let \( G \) be a topological group. Then \( G \) is profinite if and only if \( G \cong \varprojlim_{i \in I} G_i \), where \( \{ G_i \}_{i \in I} \) is an inverse system of finite, discrete groups.
Proof Observe first of all that \( \varprojlim_{i \in I} G_i \) is a closed subspace of the product \( \prod_{i \in I} G_i \). Indeed the inverse limit is defined as the set of sequences \( (a_i) \in \prod_{i \in I} G_i \) such that for every map \( \phi_{i,j} \colon G_i \to G_j \) of the inverse system we have that \( \phi_{i,j}(a_i) = a_j \). Hence \( \varprojlim_{i \in I} G_i \) is the intersection of the subspaces of \( \prod_{i \in I} G_i \) obtained as \( (\varphi_{i,j})^{-1}(\Delta_j) \) where \[ \varphi_{i,j} \colon \prod_{k \in I} G_k \twoheadrightarrow G_i \times G_j \xrightarrow{\phi_{i,j} \times \operatorname{Id}} G_j \times G_j \] and \( \Delta_j \subseteq G_j \times G_j \) is the diagonal. Observe now that every finite, discrete group \( G_i \) is trivially a Stone space. This implies that \( \varprojlim_{i \in I} G_i \) is a closed subset of a product of Stone spaces, and thus it is a Stone space itself. This follows from the fact that the product of Hausdorff spaces is Hausdorff (see this question on Math StackExchange), the product of compact spaces is compact (by Tychonoff's theorem) and the product of totally disconnected spaces is totally disconnected (see this question on Math StackExchange), and the fact that all these properties are preserved by closed sub-spaces. This shows that \( \varprojlim_{i \in I} G_i \) is profinite, and thus that \( G \) is profinite if it is an inverse limit of finite, discrete groups.
Vice versa, suppose that \( G \) is profinite. Observe that we have a continuous group homomorphism \( G \to \widehat{G} \) given by sending each element \( g \in G \) to the "constant sequence" \( (\pi_H(g))_H \in \widehat{G} \), where \( \pi_H \colon G \to G/H \) is the quotient map. We would like to prove that this continuous map is a homeomorphism, and since both \( G \) and \( \widehat{G} \) are compact and Hausdorff it is sufficient to show that this map is bijective (see Lemma B6.7 of these notes by Tom Leinster). First of all, we prove surjectivity. Let \( \{ g_H \}_H \subseteq G \) be a sequence of elements indexed on the finite-index, normal subgroups of \( G \) such that \( (\pi_H(g_H))_H \in \widehat{G} \). Then by Exercise 4 the cosets \( g_H H \subseteq G \) are all non-empty closed subsets, and for every two finite-index, normal subgroups \( H,K \trianglelefteq G \) we have that \( g_H H \cap g_K K \supseteq g_{H \cap K} (H \cap K) \). This implies that \( \bigcap_H g_H H \neq \emptyset \), by Cantor's intersection theorem. To conclude it is sufficient to observe that for every \( g \in \bigcap_H g_H H \) we have that \( \overline{g} = \pi_H(g_H) \) for all normal subgroups of finite index \( H \trianglelefteq G \). This proves indeed that the image of \( g \) under the map \( G \to \widehat{G} \) is equal to \( (\pi_H(g_H))_H \), and thus that the map is surjective.
To conclude, we want to prove injectivity. Observe that \( (\pi_H(g))_H = 1 \) in \( \widehat{G} \) if and only if \( g \in \bigcap_H H \). Thus to conclude we have to prove that \( \bigcap_H H = \{ 1 \} \). The proof of this result is rather technical, and we will omit it from these notes. If you are interested you can read Lemma 3.9 of these notes by Brian Osserman. Q.E.D.
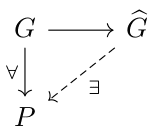
The previous theorem tells us in particular that for every map of topological groups \( G \to P \), where \( P \) is profinite, there exists a unique map of topological groups \( \widehat{G} \to P \) such that the triangle on the right commutes (this is the universal property of the profinite completion).
Exercise 4 Let \( G \) be a topological group, and \( H \leq G \) be a subgroup. Prove that if \( H \) is open then \( H \) is also closed. Moreover, prove that if \( G \) is compact then \( H \) is open if and only if it is closed and has finite index.
The previous theorem tells us that a topological group is "pro-finite" if and only if it is the (inverse) limit of a system of finite groups considered with the discrete topology.
Example 5 Let \( K \subseteq L \) be a Galois extension of field. We have already seen that \( L \) is the direct limit of all the sub-extensions \( K \subseteq M \subseteq L \) such that \( K \subseteq M \) is finite. From this we get that \[ \operatorname{Gal}(L/K) \cong \varprojlim_{\substack{K \subseteq M \subseteq L \\ [M \colon K] < \infty}} \operatorname{Gal}(M/K) \] which implies that the group \( \operatorname{Gal}(L/K) \) is a profinite topological group.
Remark 6 Observe that taking only open normal subgroups of finite index in the definition of completion is necessary. Equivalently, we cannot expect that a profinite group is isomorphic to the profinite completion of itself regarded with the discrete topology. For example in the absolute Galois group \( G_{\mathbb{Q}} \) there are an infinite number of non-open normal subgroups of finite index (see Proposition 7.26 of these notes by James S. Milne). Thanks to a deep theorem of Nikolay Nikolov and Dan Segal (see their papers on this here and here) this implies that \( G_{\mathbb{Q}} \) is not topologically finitely generated, i.e. it is not the closure of a finitely generated subgroup (see also this question on MathOverflow, where the term "profinite completion" does not require the subgroups in the inverse limit to be open).
The local Artin map
Recall from the previous lecture that the local version of the theorem of Kronecker and Weber allows us to compute that \( G_{\mathbb{Q}_p}^{\text{ab}} \cong \mathbb{Z}_p^{\times} \times \widehat{\mathbb{Z}} \). Observe in particular that \( \mathbb{Z}_p^{\times} \times \widehat{\mathbb{Z}} \cong \widehat{\mathbb{Q}_p^{\times}} \), because we have that \( \mathbb{Q}_p^{\times} \cong \mathbb{Z}_p^{\times} \times \mathbb{Z} \) and \( \mathbb{Z}_p^{\times} \) is already profinite.The main result of local class field theory is that this is true for every local field (see Definition 12 of the ninth lecture).
Theorem 7 Let \( K \) be a local field. Then there exists a unique surjective homomorphism of topological groups \( \theta \colon K^{\times} \to G_K^{\text{ab}} \) (called local Artin map) such that:
- if \( K \) is non-Archimedean then for every finite, unramified extension \( K \subseteq L \) (which is abelian by Corollary 2 of the thirteenth lecture) the composition of maps \[ K^{\times} \xrightarrow{\theta} G_K^{\text{ab}} \twoheadrightarrow \operatorname{Gal}(L/K) \xrightarrow{\sim} \operatorname{Gal}(\kappa_L/\kappa_K) \] sends every uniformizer \( \pi \in K^{\times} \) to the Frobenius automorphism \( \kappa_L \to \kappa_L \) defined by \( x \mapsto x^q \), where \( q = \# \kappa_{K} \);
- if \( K \subseteq L \) is a finite extension we have that the diagram on the right is commutative, where \( \operatorname{N}_{L/K} \colon L^{\times} \to K^{\times} \) is the field norm and the map \( G_L^{\text{ab}} \to G_K^{\text{ab}} \) is given by restricting an automorphism \( \sigma \colon L^{\text{ab}} \to L^{\text{ab}} \) to \( K^{\text{ab}} \).

This theorem can be proved in many ways: using the Brauer group of a field (as Helmut Hasse did), using Galois cohomology (as Emil Artin did), using formal groups (as Jonathan Lubin and John Tate did) or using explicit approaches (as Jürgen Neukirch and Michael Hazewinkel did). For now, we will only content ourselves with drawing some consequences from this theorem and proving the last part.
Observe first of all that if \( K \subseteq L \) is a finite abelian extension we have a surjective map \[ K^{\times} \xrightarrow{\theta} G_K^{\text{ab}} \twoheadrightarrow \operatorname{Gal}(L/K) \] whose kernel coincides with \( \operatorname{N}_{L/K}(L^{\times}) \subseteq K^{\times} \). Indeed observe that \( L \subseteq K^{\text{ab}} \), which implies, by Galois theory, that \( G_L^{\text{ab}} = \operatorname{Gal}(K^{\text{ab}}/L) \). Thus we get an exact sequence \[ \{1\} \to G_L^{\text{ab}} \to G_K^{\text{ab}} \to \operatorname{Gal}(L/K) \to \{ 1 \} \] where the first map is precisely the restriction map described in the second point of the theorem. Thus using the commutativity of the diagram above and the fact that \( \theta \) is surjective we get that for every element \( x \in K^{\times} \) the automorphism \( \theta(x) \in G_K^{\text{ab}} \) becomes trivial in \( \operatorname{Gal}(L/K) \) if and only if \( x \in \operatorname{N}_{L/K}(L^{\times}) \).
Norm groups
The Artin map that we mentioned in Theorem 6 is a surjective, continuous group homomorphism \( \theta \colon K^{\times} \to G_K^{\text{ab}} \), but it cannot be an isomorphism because the group \( G_K^{\text{ab}} \) is profinite, whereas \( K^{\times} \) is not. Indeed, we have that \( K^{\times} \cong A_K^{\times} \times \mathbb{Z} \) because for every uniformizer \( \pi \in K \) we can write \( K^{\times} = \pi^{\mathbb{Z}} \times A_K^{\times}\).Nevertheless, we can apply the universal property of the profinite completion to get a map \( \widehat{\theta} \colon \widehat{K^{\times}} \to G_K^{\text{ab}} \), and we could hope that this map is an isomorphism. Since the Artin map is already continuous and surjective, we only need to prove that \( \widehat{\theta} \) is injective.
This is equivalent to show that every open, normal subgroup of \( K^{\times} \) of finite index corresponds to an open, normal subgroup of \( G_K^{\text{ab}} \) of finite index. Galois theory tells us that these subgroups correspond to finite abelian extensions \( K \subseteq L \), and in turn we have seen in the previous paragraph that \( \theta^{-1}(\operatorname{Gal}(K^{\text{ab}}/L)) = \operatorname{N}_{L/K}(L^{\times}) \). Thus, proving that \( \widehat{\theta} \) is injective is equivalent to prove the following theorem.
Theorem 8 Let \( K \) be a local field. For every open normal subgroup of finite index \( U \trianglelefteq K^{\times} \) there exists a unique finite abelian extension \( K \subseteq L \) such that \( U = \operatorname{N}_{L/K}(L^{\times}) \).
Proof The uniqueness part is clear using Theorem 7 and Galois theory. If \( K \) is Archimedean, the statement is easy to prove (see Exercise 9 and Exercise 10), thus we will from now on assume that \( K \) is non-Archimedean. In this case, the proof of the existence part of the theorem uses the following facts:
- \( D_K := \bigcap_{L} \operatorname{N}_{L/K}(L^{\times}) = \{ 1 \} \), where \( L \) runs over all the finite abelian extensions of \( K \). To prove this, one proves first of all that \( D_K \) is divisible, i.e. that \( n D_K = D_K \) for all \( n \in \mathbb{N}_{\geq 1} \). This can be done using Kummer theory when \( K \) has characteristic zero (i.e. \( K \) is a finite extension of \( \mathbb{Q}_p \)), and needs some clever argument when \( K \) has positive characteristic (see Proposition 6 (page 174) and Propositon 16 of page 217 of the book "Local fields" by Jean-Pierre Serre). This implies that \( D_K \) would be contained in every subgroup of finite index (if \( I \leq K^{\times} \) has index \( n \) then \( n D_K = D_K \subseteq n K^{\times} \subseteq I \)) and thus in particular \[ D_K \subseteq \bigcap_{m,n} U_K^{(m)} \cdot \pi^{n \mathbb{Z}} = \{ 1 \} \] where \( U_K^{(m)} \leq A_K^{\times} \) are the unit groups defined in Theorem 4 of the fourteenth lecture;
- if \( I \leq K^{\times} \) is a subgroup of finite index which contains \( A_K^{\times} \), then there exists a finite abelian extension \( K \subseteq L \) such that \( I = \operatorname{N}_{L/K}(L^{\times}) \). This is easier than the previous fact. Indeed, if \( I \) has index \( n \) and contains \( A_K^{\times} \) we claim that \( \operatorname{N}(K_n/K)(K_n^{\times}) \subseteq I \), where \( K \subseteq K_n \) is the unique unramified extension of degree \( n \) (see Corollary 2 of the thirteenth lecture). This happens because the valuation map \( v_K \colon K^{\times} \to \mathbb{Z} \) is surjective and has kernel \( A_K^{\times} \), which implies that \( I = v_K^{-1}(n \mathbb{Z}) \), and finally we have that \[ \operatorname{N}(K_n/K)(K_n^{\times}) \subseteq v_K^{-1}(v_K(\operatorname{N}(K_n/K)(K_n^{\times}))) = v_K^{-1}(n \mathbb{Z}) = I \] where we use the facts that \( v_K(\operatorname{N}(K_n/K)(K_n^{\times})) = n \mathbb{Z} \) and \( A_K^{\times} \subseteq \operatorname{N}(K_n/K)(K_n^{\times}) \). The first fact is easy to prove, because any uniformizer \( \pi \in K \) is also a uniformizer for \( K_n \), and thus every element of \( K_n \) can be written as \( \pi^m x \) with \( m \in \mathbb{Z} \) and \( x \in A_{K_n}^{\times} \), which implies that \( v_K(\operatorname{N}(K_n/K)(\pi^m x)) = v_K(\pi^{n m}) = n m \in n \mathbb{Z} \). The second fact can be proved using Hilbert's theorem 90 (see Proposition 1.2 of Chapter 3 of these notes by James S. Milne).
Actually, we have that \( I \supseteq \operatorname{N}_{L/K}(L^{\times}) \cap (A_K^{\times} \cdot (\operatorname{N}_{L/K}(L^{\times}) \cap I)) \) because if \( a \in \operatorname{N}_{L/K}(L^{\times}) \cap (A_K^{\times} \cdot (\operatorname{N}_{L/K}(L^{\times}) \cap I)) \) then we can write \( a = b \, c \) with \( b \in A_K^{\times} \) and \( c \in \operatorname{N}_{L/K}(L^{\times}) \cap I \), which implies that \( b = a c^{-1} \in \operatorname{N}_{L/K}(L^{\times}) \) and thus that \( a \in \operatorname{N}_{L/K}(L^{\times}) \cap A_K^{\times} \subseteq I \).
Since \( A_K^{\times} \cdot (\operatorname{N}_{L/K}(L^{\times}) \cap I) \) contains \( A_K^{\times} \) we can use the second fact to find a finite abelian extension \( K \subseteq E \) such that \( \operatorname{N}_{E/K}(E^{\times}) = A_K^{\times} \cdot (\operatorname{N}_{L/K}(L^{\times}) \cap I) \subseteq I \). Thus we can use Galois theory and the fact that \( \operatorname{Gal}(E/K) \cong K^{\times}/\operatorname{N}_{E/K}(E^{\times}) \) from Theorem 7 to find an intermediate extension \( K \subseteq F \subseteq E \) such that \( I = \operatorname{N}_{F/K}(F^{\times}) \), which is what we wanted to prove. Q.E.D.
Exercise 9 Prove that \( \mathbb{C}^{\times} \) has no non-trivial open subgroups. (Hint: use Exercise 4).
Exercise 10 Prove that the only non-trivial open subgroup of \( \mathbb{R}^{\times} \) is \( \mathbb{R}_{> 0} \). (Hint: use again Exercise 4).
Conclusions and references
In this lecture we managed to:- recall a few facts on profinite groups, including the definition of the profinite completion of a topological group;
- state the main theorem of local class field theory (Theorem 7);
- prove the existence theorem of local class field theory (Theorem 8) almost completely (we are missing the proof of the fact that \( D_K \) is divisible and that \( A_K^{\times} \subseteq \operatorname{N}(K_n/K)(K_n^{\times}) \));
- these notes by Andrew Sutherland;
- this summary by Bjorn Poonen;
- Section III.3 and Section III.5 of the notes "Class field theory" by James S. Milne;
- the article "Local class field theory" by Jean-Pierre Serre, printed as Chapter VI in the book "Algebraic number theory" edited by John W.S. Cassels and Albrecht Fröhlich;
- Chapter XI and Chapter XIV of the book "Local fields" by Jean-Pierre Serre;
- Chapter IV of the book "Local fields and their extensions" by Ivan Fesenko and Sergeĭ Vladimirovich Vostokov;
- Chapter V of the book "Algebraic number theory" by Jürgen Neukirch.

Comments
Post a Comment