TANT 15 - Abhyankar's lemma and local Kronecker-Weber
Hello there! These are notes for the fifteenth class of the course "Topics in algebra and number theory" held in Block 4 of the academic year 2017/18 at the University of Copenhagen.
In the previous lecture we have defined the ramification filtration of a finite, Galois extension of complete, discretely valued fields. This filtration gives us a way of studying the Galois group of any extension of complete, discretely valued fields. In this lecture we will concentrate on Galois extensions of a local field that are abelian, i.e. the Galois group is commutative. In particular we will see that every (tamely ramified) abelian extension of \( \mathbb{Q}_{p} \) is contained in a cyclotomic extension.
In order to do so, we will need a lemma which will enable us to kill the ramification in an extension of valued fields after changing the base field: this is the so-called Abhyankhar's lemma.
Lemma 1 Consider the diagram of discretely valued fields on the right, where \( K \subseteq L \) is finite and unramified. Then \( E \subseteq E L \) is also finite and unramified.
Proof We can assume that everything is complete, because completing preserves finite extensions (see Exercise 5 of the twelfth lecture) and preserves the value groups when the fields are non-Archimedean (see Exercise 2 of the ninth lecture). Moreover, we can assume that \( K = L \cap E \) because the extension \( L \cap E \subseteq L \) is also unramified.
Now, since everything is complete we can apply Theorem 1 of the thirteenth lecture to see that there exists a polynomial \( f(x) \in K[x] \) such that its reduction \( \overline{f}(x) \in \kappa_{K}[x] \) is separable and \( L \cong K[x]/(f(x)) \). Moreover, since \( K = L \cap E \) we have that \( EL \cong E[x]/(f(x)) \) and this concludes the proof because the polynomial \( \overline{f}(x) \in \kappa_{E}[x] \) is still separable. Q.E.D.
Remark 2 In the proof of the previous lemma we have introduced new notation. Namely, if \( (K,\phi) \) is a non-Archimedean valued field sometimes we will omit \( \phi \) and we will write \( A_K \) for the valuation ring, \( \mathfrak{m}_K \) for the maximal ideal and \( \kappa_{K} \) for the residue field.
Using the previous lemma we can prove a powerful result on tamely ramified extensions, which goes under the name of Abhyankar's lemma.
Theorem 2 Let \( (K,\phi) \) be a discretely valued field and let \( K \subseteq L \subseteq M \) and \( K \subseteq E \subseteq M \) be finite field extensions. Suppose that \( K \subseteq L \) is tamely ramified and that \( e(L \mid K) \) divides \( e(E \mid K) \). Then \( E \subseteq L E \) is unramified.
Proof Again as before, we may assume that everything is complete. Let \( L_0 \subseteq L \) be the inertia field of the extension \( K \subseteq L \) (see Lemma 7 of the thirteenth lecture). Then \( K \subseteq L_0 \) is unramified (i.e. \( e(L_0 \mid K) = 1 \) ), and thus we can apply the previous lemma to see that \( E \subseteq L_0 E \) is unramified, i.e. \( e(L_0 E \mid E) = 1 \). Thus we can use the multiplicativity of the ramification and inertia indexes (see Exercise 3) to see that \( E \subseteq L E \) is unramified if and only if \( L_0 E \subseteq L E \) is unramified.
Observe now that the extension \( L_0 \subseteq L \) is tamely and totally ramified, because \( L_0 \) is the inertia field of the extension \( K \subseteq L \). Thus we can apply Theorem 6 of the thirteenth lecture to see that \( L = L_0(\sqrt[e]{\pi_{L_0}}) \) for some uniformizer \( \pi_{L_0} \in L_0 \), where \( e = e(L \mid K) = e(L \mid L_0) = [L \colon L_0] \). Let now \( \pi_{L_0 E} \in L E \) be any uniformizer and recall that \( \pi_{L_0 E}^{e(L_0 E \, \mid \, L_0)}/\pi_{L_0} \in A_{L_0}^{\times} \). We can now use the fact that \( e = e(L \mid K) \) divides \( e(E \mid K) = e(L_0 E \mid L_0) \) to write \( e(L_0 E \mid L_0) = e \, e' \) and get that \[ \frac{\pi_{L_0}}{\pi_{L_0 E}^{e(L_0 E \, \mid \, L_0)}} = \left( \frac{\sqrt[e]{\pi_{L_0}}}{\pi_{L_0 E}^{e'}} \right)^e = u \in A_{L_0}^{\times} \] which implies that \( L E = L_0 E(\sqrt[e]{\pi_{L_0}}) = L_0 E(\sqrt[e]{u}) \) for \( u \in A_{L_0}^{\times} \). Let now \( f(x) := x^e - u \in A_{L_0}[x] \) and observe that \( \overline{f}(x) \in \kappa_{L_0}[x] \) is separable because \( \overline{u} \neq 0 \) and the characteristic of \( \kappa_{L_0} \) equals the characteristic of \( \kappa_{K} \), which is coprime to \( e \) by hypothesis. Thus we may invoke again Theorem 1 of the thirteenth lecture to see that \( L_0 E \subseteq L E \) is unramified and conclude. Q.E.D.
Exercise 3 Prove that the ramification and the inertia index are multiplicative. More precisely, if \( K \subseteq L \subseteq M \) are extensions of non-Archimedean valued fields, we have that \( e(M \mid K) = e(M \mid L) e(L \mid K) \) and \( f(M \mid K) = f(M \mid L) f(L \mid K) \).
Exercise 4 Prove that the group of roots of unity \( \mu_n(\mathbb{Q}_p) \leq \mathbb{Q}_p^{\times} \) is a cyclic group of order equal to \( \gcd(n,p-1) \) if \( p \geq 3 \) and of order equal to \( \gcd(n,2) \) if \( p = 2 \). (Hint: prove a similar statement for \( \mu_n(\mathbb{F}_p) \) and use Hensel's lemma when \( p \nmid n\). If \( p \mid n \) you need to do a little more... See for example Theorem 3.1 of these notes by Keith Conrad).
Example 5 Let \( m \in \mathbb{N} \) and suppose that \( p \nmid m \). Then the reduction of the \( m \)-th cyclotomic polynomial \( \Phi_m(x) \) modulo \( p \) is separable, and thus we can apply Theorem 1 of the thirteenth lecture to see that the extension \( \mathbb{Q}_p \subseteq \mathbb{Q}_p(\zeta_m) \) is unramified. Moreover, if \( d = [\mathbb{Q}_p(\zeta_m) \colon \mathbb{Q}_p] \) we know from Corollary 2 of the thirteenth lecture that \( \mathbb{Q}_p(\zeta_m) = \mathbb{Q}_p(\zeta_{p^d - 1}) \). Finally, since this extension is unramified we know from Theorem 1 of the previous lecture that \( \operatorname{Gal}(\mathbb{Q}_p(\zeta_{p^d - 1})/\mathbb{Q}_p) \cong \operatorname{Gal}(\mathbb{F}_p(\zeta_{p^d - 1})/\mathbb{F}_p) \cong \mathbb{Z}/d \mathbb{Z} \).
Example 6 Consider now the cyclotomic extension \( \mathbb{Q}_p \subseteq \mathbb{Q}_p(\zeta_{p^r}) \) for some \( r \in \mathbb{N} \), and assume that \( p \geq 3 \). We see from Exercise 4 that this extension has order \( p^{r-1} \cdot (p - 1) \). Moreover, the situation is exactly like the one we have over \( \mathbb{Q} \), and in particular we have that \[ \operatorname{Gal}(\mathbb{Q}_p(\zeta_{p^r})/\mathbb{Q}_p) \cong \left( \frac{\mathbb{Z}}{p^r \mathbb{Z}} \right)^{\times} \cong \frac{\mathbb{Z}}{p^{r - 1} \mathbb{Z}} \times \frac{\mathbb{Z}}{(p - 1) \mathbb{Z}} \] (see Theorem 2.3 and Theorem 2.5 of these notes by Keith Conrad).
Observe now that \( 1 - \zeta_{p^r} \in \mathbb{Q}_p(\zeta_{p^r}) \) is a uniformizer. Indeed its minimal polynomial is \( \Phi_{p^r}(1 - x) \) and we have that \( \Phi_{p^r}(x) = \sum_{j = 0}^{p - 1} x^{j p^{r - 1}} \), which implies that \( \operatorname{N}_{\mathbb{Q}_p(\zeta_{p^r})/\mathbb{Q}_p}(1 - \zeta_{p^r}) = \Phi_{p^r}(1) = p \). This implies immediately that \( 1 - \zeta_{p^r} \) is a uniformizer of \( \mathbb{Q}_p(\zeta_{p^r}) \) by the description of the absolute value on \( \mathbb{Q}_p(\zeta_{p^r}) \) given by Theorem 1 of the twelfth lecture and the fact that \( p \in \mathbb{Q}_p \) is a uniformizer.
Moreover, it is not difficult to see that the polynomial \( \Phi_{p^r}(1 - x) \) is Eisenstein, and thus that the extension \( \mathbb{Q}_p \subseteq \mathbb{Q}_p(\zeta_{p^r}) \) is totally ramified.
Finally, Hensel's lemma shows that \( \mathbb{Q}_p(\zeta_{p}) \cong \mathbb{Q}_p[x]/(x^{p-1} + p) \), but the analogous statement is false for \( r \geq 2 \). Indeed, the extension \( \mathbb{Q}_3 \subseteq \mathbb{Q}_3[x]/(x^{6} + 3) \) is Galois, but its Galois group is isomorphic to \( S_3 \) and not to \( \mathbb{Z}/2 \mathbb{Z} \times \mathbb{Z}/3 \mathbb{Z} \cong \mathbb{Z}/6 \mathbb{Z} \) as can be seen here.
Finally, if \( p = 2 \) then again the situation is analogous to what happens over \( \mathbb{Q} \), and we have that \[ \operatorname{Gal}(\mathbb{Q}_2(\zeta_{2^r})/\mathbb{Q}_2) \cong (\mathbb{Z}/2^r \mathbb{Z})^{\times} \cong \frac{\mathbb{Z}}{2 \mathbb{Z}} \times \frac{\mathbb{Z}}{2^{r - 2} \mathbb{Z}} \] if \( r \geq 2 \), whereas \( \mathbb{Q}_2(\zeta_2) = \mathbb{Q}_2 \). Again the same argument as before shows that this extension is totally ramified.
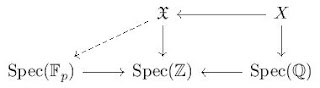
Example 7 In general, if \( n \in \mathbb{N} \) we can write \( n = m p^r \) with \( p \nmid m \) and we have that the extension \( \mathbb{Q}_p(\zeta_n) = \mathbb{Q}_p(\zeta_m) \mathbb{Q}_p(\zeta_{p^r}) \) where \( \mathbb{Q}_p \subseteq \mathbb{Q}_p(\zeta_m) \subseteq \mathbb{Q}_p(\zeta_n) \) is the inertia field. The picture to have in mind is the following:
We are now ready to proceed towards the proof of the local theorem of Kronecker and Weber.
Lemma 8 Let \( \mathbb{Q}_p \subseteq K \) be a finite, Galois extension and suppose that \( \operatorname{Gal}(K/\mathbb{Q}_p) \) is cyclic of order \( q^r \) where \( q \in \mathbb{N} \) is a prime and \( q \neq p \). Then there exists \( m \in \mathbb{N} \) such that \( K \subseteq \mathbb{Q}_p(\zeta_m) \), where \( \zeta_m \) is a primitive \( m \)-th root of unity, i.e. \( \mathbb{Q}_p(\zeta_m) \cong \mathbb{Q}_p[x]/(\Phi_m(x)) \) where \( \Phi_m(x) \in \mathbb{Z}[x] \) is the \( m \)-th cyclotomic polynomial.
Proof First of all, \( \mathbb{Q}_p \subseteq K \) is tamely ramified because we know from Theorem 10 of the twelfth lecture that \( e(K \mid \mathbb{Q}_p) \) divides \( q^n \), and thus \( p \nmid e(K \mid \mathbb{Q}_p) \). This implies that \( I^w(K \mid \mathbb{Q}_p) \) is trivial and thus we can use Corollary 5 of the fourteenth lecture to see that \( I(K \mid \mathbb{Q}_p) \) can be embedded into \( \mathbb{F}_p^{\times} \). Thus \( \mathbb{Q}_p \subseteq K \) is tamely ramified and \( e(K \mid \mathbb{Q}_p) \) divides \( p - 1 \), which is the ramification index of the extension \( \mathbb{Q}_p \subseteq \mathbb{Q}_p(\zeta_p) \) by the previous example. Hence Theorem 2 tells us that the extension \( \mathbb{Q}_p(\zeta_p) \subseteq K(\zeta_p) \) is an unramified extension of non-Archimedean local fields. Then Corollary 2 of the thirteenth lecture tells us that \( K(\zeta_p) = \mathbb{Q}_p(\zeta_p,\zeta) \) for some root of unity \( \zeta \) whose order \( n \) is coprime to \( p \). Thus if we take \( m = n p \) we have that \( K \subseteq \mathbb{Q}_p(\zeta_m) \). Q.E.D.
Theorem 9 Let \( \mathbb{Q}_p \subseteq K \) be a finite, Galois extension and suppose that \( \operatorname{Gal}(K/\mathbb{Q}_p) \) is an abelian group and that \( p \nmid \# \operatorname{Gal}(K/\mathbb{Q}_p) \). Then there exists \( n \in \mathbb{N} \) such that \( K \subseteq \mathbb{Q}_p(\zeta_n) \).
Proof We can use the fundamental theorem of finite abelian groups (see also this paper of Gabriel Navarro) to write \( \operatorname{Gal}(K/\mathbb{Q}_p) = C_1 \times \cdots \times C_r \) where the \( C_j \)'s are cyclic groups of prime power order. Thus we can apply Lemma 8 to the extensions \[ \mathbb{Q}_p \subseteq K_j \qquad \text{where} \qquad K_j := K^{C_1 \times \cdots \times \widehat{C_j} \times \cdots \times C_r} \] whose Galois group is isomorphic to \( C_j \). Then we get that \( K_j \subseteq \mathbb{Q}_p(\zeta_{m_j} \) and all the \( m_j \)'s are coprime. Thus \( K = K_1 \cdots K_r \subseteq \mathbb{Q}_p(\zeta_n) \) where \( n = m_1 \cdots m_r \). Q.E.D.
The previous theorem is valid also without the hypothesis that \( p \nmid \# \operatorname{Gal}(K/\mathbb{Q}_p) \). To prove this it is clearly sufficient to apply again the fundamental theorem of finite abelian groups and the following lemma.
Lemma 10 Let \( \mathbb{Q}_p \subseteq K \) be a finite, Galois extension and suppose that \( \operatorname{Gal}(K/\mathbb{Q}_p) \) is cyclic of order \( p^r \). Then there exists \( m \in \mathbb{N} \) such that \( K \subseteq \mathbb{Q}_p(\zeta_m) \).
Proof We will prove that we can take \( m = (p^{p^r} - 1) p^{r + 1} \) if \( p \geq 3 \). Indeed suppose by contradiction that \( K \not\subseteq \mathbb{Q}_p(\zeta_m) \). Then we have that \( \{ 1 \} \neq \operatorname{Gal}(K(\zeta_m)/\mathbb{Q}_p(\zeta_m)) \hookrightarrow \operatorname{Gal}(K/\mathbb{Q}_p) \) and thus \( \operatorname{Gal}(K(\zeta_m)/\mathbb{Q}_p(\zeta_m)) \) is a cyclic group of order \( p^s \) with \( 0 < s \leq r \). Using this we get that \[ \operatorname{Gal}(K(\zeta_m)/\mathbb{Q}_p) \cong \operatorname{Gal}(K(\zeta_m)/\mathbb{Q}_p(\zeta_m)) \times \operatorname{Gal}(\mathbb{Q}_p(\zeta_m)/\mathbb{Q}_p) \cong \frac{\mathbb{Z}}{p^s \mathbb{Z}} \times \frac{\mathbb{Z}}{p^r \mathbb{Z}} \times \frac{\mathbb{Z}}{p^r \mathbb{Z}} \times \frac{\mathbb{Z}}{(p - 1) \mathbb{Z}} \] because \( \operatorname{Gal}(\mathbb{Q}_p(\zeta_{p^{r + 1}})/\mathbb{Q}_p) \cong (\mathbb{Z}/p^{r +1} \mathbb{Z})^{\times} \) as it happens over \( \mathbb{Q} \) (see Example 5) and \( \operatorname{Gal}(\mathbb{Q}_p(\zeta_{p^{p^r} - 1})/\mathbb{Q}_p) \cong \mathbb{Z}/p^r \mathbb{Z} \) (see Example 6). Thus \( \operatorname{Gal}(K(\zeta_m)/\mathbb{Q}_p) \) is an abelian group with a (normal) subgroup isomorphic to \( (\mathbb{Z}/p \mathbb{Z})^3 \), and this implies that there exists a sub-extension \( \mathbb{Q}_p \subseteq L \subseteq K(\zeta_m) \) with \( \operatorname{Gal}(L/\mathbb{Q}_p) \cong (\mathbb{Z}/p \mathbb{Z})^3 \) which is impossible if \( p \geq 3 \), as we will prove in the first lecture of the last week using Kummer theory.
This proof would hold also for \( p = 2 \), but the problem is that \( \operatorname{Gal}(\mathbb{Q}_2(\zeta_{24})/\mathbb{Q}_2) \cong (\mathbb{Z}/2 \mathbb{Z})^3 \). Thus we need to be a little more careful, and to take \( m = (2^{2^r} - 1) 2^{r + 2} \). Supposing again by contradiction that \( K \not\subseteq \mathbb{Q}_2(\zeta_m) \) we would have that
\[ \operatorname{Gal}(K(\zeta_m)/\mathbb{Q}_2) \cong \begin{cases} \frac{\mathbb{Z}}{2^s \mathbb{Z}} \times \frac{\mathbb{Z}}{2^r \mathbb{Z}} \times \frac{\mathbb{Z}}{2^r \mathbb{Z}} \times \frac{\mathbb{Z}}{2 \mathbb{Z}}, \ \text{for some} \ 0 < s \leq r \\ \text{or} \\ \frac{\mathbb{Z}}{2^s \mathbb{Z}} \times \frac{\mathbb{Z}}{2^r \mathbb{Z}} \times \frac{\mathbb{Z}}{2^r \mathbb{Z}}, \ \text{for some} \ 2 \leq s \leq r \end{cases} \] and this implies that there exists a sub-extension \( \mathbb{Q}_2 \subseteq L \subseteq K(\zeta_m) \) with \( \operatorname{Gal}(L/\mathbb{Q}_2) \cong (\mathbb{Z}/2 \mathbb{Z})^4 \) (in the first case) or \( \operatorname{Gal}(L/\mathbb{Q}_2) \cong (\mathbb{Z}/4 \mathbb{Z})^3 \) (in the second case), and we will show again in the first lecture of the last week that this is impossible by means of Kummer theory. Q.E.D.
Thus, as a corollary, we get the important local theorem of Kronecker and Weber:
Corollary 11 Every finite abelian extension of \( \mathbb{Q}_p \) is contained in a cyclotomic field.
In the previous lecture we have defined the ramification filtration of a finite, Galois extension of complete, discretely valued fields. This filtration gives us a way of studying the Galois group of any extension of complete, discretely valued fields. In this lecture we will concentrate on Galois extensions of a local field that are abelian, i.e. the Galois group is commutative. In particular we will see that every (tamely ramified) abelian extension of \( \mathbb{Q}_{p} \) is contained in a cyclotomic extension.
In order to do so, we will need a lemma which will enable us to kill the ramification in an extension of valued fields after changing the base field: this is the so-called Abhyankhar's lemma.
Abhyankhar's lemma
Let's start with a preliminary result on the composition of unramified extensions.
Proof We can assume that everything is complete, because completing preserves finite extensions (see Exercise 5 of the twelfth lecture) and preserves the value groups when the fields are non-Archimedean (see Exercise 2 of the ninth lecture). Moreover, we can assume that \( K = L \cap E \) because the extension \( L \cap E \subseteq L \) is also unramified.
Now, since everything is complete we can apply Theorem 1 of the thirteenth lecture to see that there exists a polynomial \( f(x) \in K[x] \) such that its reduction \( \overline{f}(x) \in \kappa_{K}[x] \) is separable and \( L \cong K[x]/(f(x)) \). Moreover, since \( K = L \cap E \) we have that \( EL \cong E[x]/(f(x)) \) and this concludes the proof because the polynomial \( \overline{f}(x) \in \kappa_{E}[x] \) is still separable. Q.E.D.
Remark 2 In the proof of the previous lemma we have introduced new notation. Namely, if \( (K,\phi) \) is a non-Archimedean valued field sometimes we will omit \( \phi \) and we will write \( A_K \) for the valuation ring, \( \mathfrak{m}_K \) for the maximal ideal and \( \kappa_{K} \) for the residue field.
Using the previous lemma we can prove a powerful result on tamely ramified extensions, which goes under the name of Abhyankar's lemma.
Theorem 2 Let \( (K,\phi) \) be a discretely valued field and let \( K \subseteq L \subseteq M \) and \( K \subseteq E \subseteq M \) be finite field extensions. Suppose that \( K \subseteq L \) is tamely ramified and that \( e(L \mid K) \) divides \( e(E \mid K) \). Then \( E \subseteq L E \) is unramified.Proof Again as before, we may assume that everything is complete. Let \( L_0 \subseteq L \) be the inertia field of the extension \( K \subseteq L \) (see Lemma 7 of the thirteenth lecture). Then \( K \subseteq L_0 \) is unramified (i.e. \( e(L_0 \mid K) = 1 \) ), and thus we can apply the previous lemma to see that \( E \subseteq L_0 E \) is unramified, i.e. \( e(L_0 E \mid E) = 1 \). Thus we can use the multiplicativity of the ramification and inertia indexes (see Exercise 3) to see that \( E \subseteq L E \) is unramified if and only if \( L_0 E \subseteq L E \) is unramified.
Observe now that the extension \( L_0 \subseteq L \) is tamely and totally ramified, because \( L_0 \) is the inertia field of the extension \( K \subseteq L \). Thus we can apply Theorem 6 of the thirteenth lecture to see that \( L = L_0(\sqrt[e]{\pi_{L_0}}) \) for some uniformizer \( \pi_{L_0} \in L_0 \), where \( e = e(L \mid K) = e(L \mid L_0) = [L \colon L_0] \). Let now \( \pi_{L_0 E} \in L E \) be any uniformizer and recall that \( \pi_{L_0 E}^{e(L_0 E \, \mid \, L_0)}/\pi_{L_0} \in A_{L_0}^{\times} \). We can now use the fact that \( e = e(L \mid K) \) divides \( e(E \mid K) = e(L_0 E \mid L_0) \) to write \( e(L_0 E \mid L_0) = e \, e' \) and get that \[ \frac{\pi_{L_0}}{\pi_{L_0 E}^{e(L_0 E \, \mid \, L_0)}} = \left( \frac{\sqrt[e]{\pi_{L_0}}}{\pi_{L_0 E}^{e'}} \right)^e = u \in A_{L_0}^{\times} \] which implies that \( L E = L_0 E(\sqrt[e]{\pi_{L_0}}) = L_0 E(\sqrt[e]{u}) \) for \( u \in A_{L_0}^{\times} \). Let now \( f(x) := x^e - u \in A_{L_0}[x] \) and observe that \( \overline{f}(x) \in \kappa_{L_0}[x] \) is separable because \( \overline{u} \neq 0 \) and the characteristic of \( \kappa_{L_0} \) equals the characteristic of \( \kappa_{K} \), which is coprime to \( e \) by hypothesis. Thus we may invoke again Theorem 1 of the thirteenth lecture to see that \( L_0 E \subseteq L E \) is unramified and conclude. Q.E.D.
Exercise 3 Prove that the ramification and the inertia index are multiplicative. More precisely, if \( K \subseteq L \subseteq M \) are extensions of non-Archimedean valued fields, we have that \( e(M \mid K) = e(M \mid L) e(L \mid K) \) and \( f(M \mid K) = f(M \mid L) f(L \mid K) \).
The (local) theorem of Kronecker and Weber
Abhyankar's lemma allows us to "kill the ramification" of any tamely ramified extension \( K \subseteq L \) if we extend the base field \( K \) to a field \( E \) whose ramification index \( e(E \mid K) \) is a multiple of \( e(L \mid K) \). This allows us immediately to prove that every tamely ramified abelian extension is cyclotomic, i.e. it is contained in \( \mathbb{Q}_p(\zeta_n) \) for some \( n \in \mathbb{N} \). Before proving this, let's have a look at the various types of cyclotomic extensions. First of all, we can see how many roots of unity are already contained in \( \mathbb{Q}_p \).Exercise 4 Prove that the group of roots of unity \( \mu_n(\mathbb{Q}_p) \leq \mathbb{Q}_p^{\times} \) is a cyclic group of order equal to \( \gcd(n,p-1) \) if \( p \geq 3 \) and of order equal to \( \gcd(n,2) \) if \( p = 2 \). (Hint: prove a similar statement for \( \mu_n(\mathbb{F}_p) \) and use Hensel's lemma when \( p \nmid n\). If \( p \mid n \) you need to do a little more... See for example Theorem 3.1 of these notes by Keith Conrad).
Example 5 Let \( m \in \mathbb{N} \) and suppose that \( p \nmid m \). Then the reduction of the \( m \)-th cyclotomic polynomial \( \Phi_m(x) \) modulo \( p \) is separable, and thus we can apply Theorem 1 of the thirteenth lecture to see that the extension \( \mathbb{Q}_p \subseteq \mathbb{Q}_p(\zeta_m) \) is unramified. Moreover, if \( d = [\mathbb{Q}_p(\zeta_m) \colon \mathbb{Q}_p] \) we know from Corollary 2 of the thirteenth lecture that \( \mathbb{Q}_p(\zeta_m) = \mathbb{Q}_p(\zeta_{p^d - 1}) \). Finally, since this extension is unramified we know from Theorem 1 of the previous lecture that \( \operatorname{Gal}(\mathbb{Q}_p(\zeta_{p^d - 1})/\mathbb{Q}_p) \cong \operatorname{Gal}(\mathbb{F}_p(\zeta_{p^d - 1})/\mathbb{F}_p) \cong \mathbb{Z}/d \mathbb{Z} \).
Example 6 Consider now the cyclotomic extension \( \mathbb{Q}_p \subseteq \mathbb{Q}_p(\zeta_{p^r}) \) for some \( r \in \mathbb{N} \), and assume that \( p \geq 3 \). We see from Exercise 4 that this extension has order \( p^{r-1} \cdot (p - 1) \). Moreover, the situation is exactly like the one we have over \( \mathbb{Q} \), and in particular we have that \[ \operatorname{Gal}(\mathbb{Q}_p(\zeta_{p^r})/\mathbb{Q}_p) \cong \left( \frac{\mathbb{Z}}{p^r \mathbb{Z}} \right)^{\times} \cong \frac{\mathbb{Z}}{p^{r - 1} \mathbb{Z}} \times \frac{\mathbb{Z}}{(p - 1) \mathbb{Z}} \] (see Theorem 2.3 and Theorem 2.5 of these notes by Keith Conrad).
Observe now that \( 1 - \zeta_{p^r} \in \mathbb{Q}_p(\zeta_{p^r}) \) is a uniformizer. Indeed its minimal polynomial is \( \Phi_{p^r}(1 - x) \) and we have that \( \Phi_{p^r}(x) = \sum_{j = 0}^{p - 1} x^{j p^{r - 1}} \), which implies that \( \operatorname{N}_{\mathbb{Q}_p(\zeta_{p^r})/\mathbb{Q}_p}(1 - \zeta_{p^r}) = \Phi_{p^r}(1) = p \). This implies immediately that \( 1 - \zeta_{p^r} \) is a uniformizer of \( \mathbb{Q}_p(\zeta_{p^r}) \) by the description of the absolute value on \( \mathbb{Q}_p(\zeta_{p^r}) \) given by Theorem 1 of the twelfth lecture and the fact that \( p \in \mathbb{Q}_p \) is a uniformizer.
Moreover, it is not difficult to see that the polynomial \( \Phi_{p^r}(1 - x) \) is Eisenstein, and thus that the extension \( \mathbb{Q}_p \subseteq \mathbb{Q}_p(\zeta_{p^r}) \) is totally ramified.
Finally, Hensel's lemma shows that \( \mathbb{Q}_p(\zeta_{p}) \cong \mathbb{Q}_p[x]/(x^{p-1} + p) \), but the analogous statement is false for \( r \geq 2 \). Indeed, the extension \( \mathbb{Q}_3 \subseteq \mathbb{Q}_3[x]/(x^{6} + 3) \) is Galois, but its Galois group is isomorphic to \( S_3 \) and not to \( \mathbb{Z}/2 \mathbb{Z} \times \mathbb{Z}/3 \mathbb{Z} \cong \mathbb{Z}/6 \mathbb{Z} \) as can be seen here.
Finally, if \( p = 2 \) then again the situation is analogous to what happens over \( \mathbb{Q} \), and we have that \[ \operatorname{Gal}(\mathbb{Q}_2(\zeta_{2^r})/\mathbb{Q}_2) \cong (\mathbb{Z}/2^r \mathbb{Z})^{\times} \cong \frac{\mathbb{Z}}{2 \mathbb{Z}} \times \frac{\mathbb{Z}}{2^{r - 2} \mathbb{Z}} \] if \( r \geq 2 \), whereas \( \mathbb{Q}_2(\zeta_2) = \mathbb{Q}_2 \). Again the same argument as before shows that this extension is totally ramified.
Example 7 In general, if \( n \in \mathbb{N} \) we can write \( n = m p^r \) with \( p \nmid m \) and we have that the extension \( \mathbb{Q}_p(\zeta_n) = \mathbb{Q}_p(\zeta_m) \mathbb{Q}_p(\zeta_{p^r}) \) where \( \mathbb{Q}_p \subseteq \mathbb{Q}_p(\zeta_m) \subseteq \mathbb{Q}_p(\zeta_n) \) is the inertia field. The picture to have in mind is the following:
We are now ready to proceed towards the proof of the local theorem of Kronecker and Weber.
Lemma 8 Let \( \mathbb{Q}_p \subseteq K \) be a finite, Galois extension and suppose that \( \operatorname{Gal}(K/\mathbb{Q}_p) \) is cyclic of order \( q^r \) where \( q \in \mathbb{N} \) is a prime and \( q \neq p \). Then there exists \( m \in \mathbb{N} \) such that \( K \subseteq \mathbb{Q}_p(\zeta_m) \), where \( \zeta_m \) is a primitive \( m \)-th root of unity, i.e. \( \mathbb{Q}_p(\zeta_m) \cong \mathbb{Q}_p[x]/(\Phi_m(x)) \) where \( \Phi_m(x) \in \mathbb{Z}[x] \) is the \( m \)-th cyclotomic polynomial.
Proof First of all, \( \mathbb{Q}_p \subseteq K \) is tamely ramified because we know from Theorem 10 of the twelfth lecture that \( e(K \mid \mathbb{Q}_p) \) divides \( q^n \), and thus \( p \nmid e(K \mid \mathbb{Q}_p) \). This implies that \( I^w(K \mid \mathbb{Q}_p) \) is trivial and thus we can use Corollary 5 of the fourteenth lecture to see that \( I(K \mid \mathbb{Q}_p) \) can be embedded into \( \mathbb{F}_p^{\times} \). Thus \( \mathbb{Q}_p \subseteq K \) is tamely ramified and \( e(K \mid \mathbb{Q}_p) \) divides \( p - 1 \), which is the ramification index of the extension \( \mathbb{Q}_p \subseteq \mathbb{Q}_p(\zeta_p) \) by the previous example. Hence Theorem 2 tells us that the extension \( \mathbb{Q}_p(\zeta_p) \subseteq K(\zeta_p) \) is an unramified extension of non-Archimedean local fields. Then Corollary 2 of the thirteenth lecture tells us that \( K(\zeta_p) = \mathbb{Q}_p(\zeta_p,\zeta) \) for some root of unity \( \zeta \) whose order \( n \) is coprime to \( p \). Thus if we take \( m = n p \) we have that \( K \subseteq \mathbb{Q}_p(\zeta_m) \). Q.E.D.
Theorem 9 Let \( \mathbb{Q}_p \subseteq K \) be a finite, Galois extension and suppose that \( \operatorname{Gal}(K/\mathbb{Q}_p) \) is an abelian group and that \( p \nmid \# \operatorname{Gal}(K/\mathbb{Q}_p) \). Then there exists \( n \in \mathbb{N} \) such that \( K \subseteq \mathbb{Q}_p(\zeta_n) \).
Proof We can use the fundamental theorem of finite abelian groups (see also this paper of Gabriel Navarro) to write \( \operatorname{Gal}(K/\mathbb{Q}_p) = C_1 \times \cdots \times C_r \) where the \( C_j \)'s are cyclic groups of prime power order. Thus we can apply Lemma 8 to the extensions \[ \mathbb{Q}_p \subseteq K_j \qquad \text{where} \qquad K_j := K^{C_1 \times \cdots \times \widehat{C_j} \times \cdots \times C_r} \] whose Galois group is isomorphic to \( C_j \). Then we get that \( K_j \subseteq \mathbb{Q}_p(\zeta_{m_j} \) and all the \( m_j \)'s are coprime. Thus \( K = K_1 \cdots K_r \subseteq \mathbb{Q}_p(\zeta_n) \) where \( n = m_1 \cdots m_r \). Q.E.D.
The previous theorem is valid also without the hypothesis that \( p \nmid \# \operatorname{Gal}(K/\mathbb{Q}_p) \). To prove this it is clearly sufficient to apply again the fundamental theorem of finite abelian groups and the following lemma.
Lemma 10 Let \( \mathbb{Q}_p \subseteq K \) be a finite, Galois extension and suppose that \( \operatorname{Gal}(K/\mathbb{Q}_p) \) is cyclic of order \( p^r \). Then there exists \( m \in \mathbb{N} \) such that \( K \subseteq \mathbb{Q}_p(\zeta_m) \).
Proof We will prove that we can take \( m = (p^{p^r} - 1) p^{r + 1} \) if \( p \geq 3 \). Indeed suppose by contradiction that \( K \not\subseteq \mathbb{Q}_p(\zeta_m) \). Then we have that \( \{ 1 \} \neq \operatorname{Gal}(K(\zeta_m)/\mathbb{Q}_p(\zeta_m)) \hookrightarrow \operatorname{Gal}(K/\mathbb{Q}_p) \) and thus \( \operatorname{Gal}(K(\zeta_m)/\mathbb{Q}_p(\zeta_m)) \) is a cyclic group of order \( p^s \) with \( 0 < s \leq r \). Using this we get that \[ \operatorname{Gal}(K(\zeta_m)/\mathbb{Q}_p) \cong \operatorname{Gal}(K(\zeta_m)/\mathbb{Q}_p(\zeta_m)) \times \operatorname{Gal}(\mathbb{Q}_p(\zeta_m)/\mathbb{Q}_p) \cong \frac{\mathbb{Z}}{p^s \mathbb{Z}} \times \frac{\mathbb{Z}}{p^r \mathbb{Z}} \times \frac{\mathbb{Z}}{p^r \mathbb{Z}} \times \frac{\mathbb{Z}}{(p - 1) \mathbb{Z}} \] because \( \operatorname{Gal}(\mathbb{Q}_p(\zeta_{p^{r + 1}})/\mathbb{Q}_p) \cong (\mathbb{Z}/p^{r +1} \mathbb{Z})^{\times} \) as it happens over \( \mathbb{Q} \) (see Example 5) and \( \operatorname{Gal}(\mathbb{Q}_p(\zeta_{p^{p^r} - 1})/\mathbb{Q}_p) \cong \mathbb{Z}/p^r \mathbb{Z} \) (see Example 6). Thus \( \operatorname{Gal}(K(\zeta_m)/\mathbb{Q}_p) \) is an abelian group with a (normal) subgroup isomorphic to \( (\mathbb{Z}/p \mathbb{Z})^3 \), and this implies that there exists a sub-extension \( \mathbb{Q}_p \subseteq L \subseteq K(\zeta_m) \) with \( \operatorname{Gal}(L/\mathbb{Q}_p) \cong (\mathbb{Z}/p \mathbb{Z})^3 \) which is impossible if \( p \geq 3 \), as we will prove in the first lecture of the last week using Kummer theory.
This proof would hold also for \( p = 2 \), but the problem is that \( \operatorname{Gal}(\mathbb{Q}_2(\zeta_{24})/\mathbb{Q}_2) \cong (\mathbb{Z}/2 \mathbb{Z})^3 \). Thus we need to be a little more careful, and to take \( m = (2^{2^r} - 1) 2^{r + 2} \). Supposing again by contradiction that \( K \not\subseteq \mathbb{Q}_2(\zeta_m) \) we would have that
\[ \operatorname{Gal}(K(\zeta_m)/\mathbb{Q}_2) \cong \begin{cases} \frac{\mathbb{Z}}{2^s \mathbb{Z}} \times \frac{\mathbb{Z}}{2^r \mathbb{Z}} \times \frac{\mathbb{Z}}{2^r \mathbb{Z}} \times \frac{\mathbb{Z}}{2 \mathbb{Z}}, \ \text{for some} \ 0 < s \leq r \\ \text{or} \\ \frac{\mathbb{Z}}{2^s \mathbb{Z}} \times \frac{\mathbb{Z}}{2^r \mathbb{Z}} \times \frac{\mathbb{Z}}{2^r \mathbb{Z}}, \ \text{for some} \ 2 \leq s \leq r \end{cases} \] and this implies that there exists a sub-extension \( \mathbb{Q}_2 \subseteq L \subseteq K(\zeta_m) \) with \( \operatorname{Gal}(L/\mathbb{Q}_2) \cong (\mathbb{Z}/2 \mathbb{Z})^4 \) (in the first case) or \( \operatorname{Gal}(L/\mathbb{Q}_2) \cong (\mathbb{Z}/4 \mathbb{Z})^3 \) (in the second case), and we will show again in the first lecture of the last week that this is impossible by means of Kummer theory. Q.E.D.
Thus, as a corollary, we get the important local theorem of Kronecker and Weber:
Corollary 11 Every finite abelian extension of \( \mathbb{Q}_p \) is contained in a cyclotomic field.
Conclusions and references
In this lecture we managed to:- prove that unramified extensions remain unramified after changing the base field;
- prove that tamely ramified extensions become unramified if we sufficiently extend the base field;
- prove the local theorem of Kronecker and Weber (up to Kummer theory, which will be the subject of next lecture).
- Section 6 of these notes by Peter Stevenhagen;
- these notes by Andrew Sutherland;
- Section 5.2 of the book "Elementary and Analytic Theory of Algebraic Numbers" by Władysław Narkiewicz;
- Chapter 14 of the book "Introduction to Cyclotomic Fields" by Lawrence C. Washington.
Comments
Post a Comment