TANT 12 - Extending absolute values
Hello there! These are notes for the twelfth class of the course "Topics in algebra and number theory" held in Block 4 of the academic year 2017/18 at the University of Copenhagen.
In the previous lecture we have seen two useful applications of completeness: Hensel's lemma, which allows us to solve equations in complete fields by solving them in their residue fields, and a characterization of norms on finite dimensional vector spaces over complete fields.
The aim of this lecture is to use the second result as a starting point to study the theory of the extensions of absolute values to an algebraic extension. We have already seen in the second lecture that if we have a field extension \( K \hookrightarrow L \) and an absolute value \( \psi \colon L \to \mathbb{R}_{\geq 0} \) we can restrict it to an absolute value \( \phi \colon K \to \mathbb{R}_{\geq 0} \).
Suppose now that we have an absolute value \( \phi \colon K \to \mathbb{R}_{\geq 0} \). Can we extend it to an absolute value \( \psi \colon L \to \mathbb{R}_{\geq 0} \)? And if we have two absolute values \( \psi_1, \psi_2 \colon L \to \mathbb{R}_{\geq 0} \) which restrict to the same absolute value on \( K \), how are they related?
It is now time to remedy to this lack and to generalize this to arbitrary finite extensions of complete fields. To do so we recall that if \( K \hookrightarrow L \) is a finite extension of fields we can define the field norm \begin{align} \operatorname{N}_{L/K} \colon L &\to K \\ \alpha &\mapsto \det_K(\mu_{\alpha}) \end{align} where \( \mu_{\alpha} \colon L \to L \) is the \( K \)-linear map defined by \( \mu_{\alpha}(x) := \alpha \, x \). Observe that the multiplicativity of the determinant immediately implies that the norm is multiplicative, i.e. \( \operatorname{N}_{L/K}(\alpha \beta) = \operatorname{N}_{L/K}(\alpha) \, \operatorname{N}_{L/K}(\beta) \) for all \( \alpha,\beta \in L \).
Theorem 1 Let \( (K,\phi) \) be a complete valued field and let \( K \hookrightarrow L \) be a finite extension of degree \( d = [L \colon K] \). Then the map \( \psi \colon L \to \mathbb{R}_{\geq 0} \) defined by \( \psi(x) := \sqrt[d]{\phi(\operatorname{N}_{L/K}(x))} \) is the unique extension of the absolute value \( \phi \) to \( L \). Moreover, \( L \) is complete with respect to \( \phi \).
Proof If \( d = 1 \) there is nothing to prove. Moreover if \( d \neq 1 \) and \( K \) is Archimedean then Theorem 16 of the fourth lecture tells us that \( d = 2 \), \( K \cong \mathbb{R} \) and \( L \cong \mathbb{C} \) and in this case this theorem is equivalent to Lemma 10 of the fourth lecture.
Suppose hence that \( (K,\phi) \) is non-Archimedean and \( d \geq 2 \). It is trivial to observe that \( \psi \) satisfies the first two axioms of Definition 1 of the second lecture. We want to check now that \( \psi(x + y) \leq \max(\psi(x),\psi(y)) \) and we know from Exercise 17 of the second lecture that this is equivalent to check that \( \psi(1 + t) \leq 1 \) for all \( t \in L \) such that \( \psi(t) \leq 1 \). Observe that for every \( x \in L \) we have that \( \operatorname{N}_{L/K}(x) = f_x(0)^{m_x} \) where \( f_x(T) \in K[T] \) is the minimal polynomial of \( x \) and \( m_x \in \mathbb{N} \). Observe moreover that \( f_{1 + x}(T) = f_x(T - 1) \) which implies that \( \psi(1 + t) \leq 1 \) if and only if \( \phi(f_t(- 1)) \leq 1 \). This would automatically follow if \( f_t(T) \in A_{\phi}[T] \).
Thus let \( t \in L \) be any element with \( \psi(t) \leq 1 \). We have that \( f_t(0) \in A_{\phi} \) because \( \psi(t) \leq 1 \) is equivalent to \( \phi(f_t(0)) \leq 1 \) and we want to prove that \( f_t \in A_{\phi} \). This follows from Hensel's lemma (see Theorem 5 of the previous lecture). Indeed if \( f_t(T) \notin A_{\phi}[T] \) then we can "clear denominators", i.e. we can find \( \alpha \in K^{\times} \) with \( \phi(\alpha) < 1 \) such that \( \alpha f_t(T) \in A_{\phi}[T] \). Observe that since \( f \) is monic and \( \phi(f_t(0)) \leq 1 \) if we write \( \alpha f_t(T) = \sum_{j = 0}^n c_j T^j \) we have that \( c_0, c_n \in \mathfrak{m}_{\phi} \). This is equivalent to say that \[ 0 < \max\{ k \, \colon \, T^k \mid \overline{\alpha f_t} \in \kappa_{\phi}[T] \} < \deg(f_t) \] and thus by Hensel's lemma there exists a polynomial \( g(T) \in A_{\phi}[T] \) such that \( \deg(g) < \deg(f_t) \) and \( g \mid f_t \). But this is absurd because the minimal polynomial \( f_t \) is irreducible.
To conclude we only have to observe that \( \psi \) is a norm on \( L \) considered as a vector space over \( K \), in the sense of Definition 8 of the previous lecture. Thus we only have to apply Theorem 14 of the previous lecture to see that \( L \) is complete with respect to \( \psi \) and that \( \psi \) is unique up to equivalence. Since \( \psi \) extends \( \phi \) we also see that \( \psi \) is unique. Q.E.D.
The proof of the previous theorem tells us that the ring \( A_{\psi} \) associated to a non-Archimedean, complete absolute value \( \psi \colon L \to \mathbb{R}_{\geq 0} \) which extends \( \phi \colon K \to \mathbb{R}_{\geq 0} \) is strongly related to \( A_{\phi} \). More precisely for every \( \alpha \in L \) we have that \( \alpha \in A_{\psi} \) if and only if \( f_{\alpha}(x) \in A_{\phi}[x] \). This property is so important that it deserves a name.
Definition 2 Let \( A \subseteq B \) be an extension of rings. Then the integral closure of \( A \) in \( B \) is the ring \( \overline{A} \subseteq B \) of all elements \( b \in B \) such that \( f(b) = 0 \) for some monic polynomial \( f(x) = x^n + a_{n - 1} x^{n - 1} + \dots + a_0 \in A[x] \).
Corollary 3 Let \( (K,\phi) \) be a non-Archimedean, complete valued field, let \( K \hookrightarrow L \) be a finite extension and let \( \psi \colon L \to \mathbb{R}_{\geq 0} \) be an absolute value extending \( \phi \). Then the ring \( A_{\psi} \subseteq L \) is the integral closure of \( A_{\phi} \) inside \( L \).
To proceed we will need to assume that this extension is separable, i.e. that for every \( \alpha \in L \) we have that \( f_{\alpha}'(x) \neq 0 \), where \( f_{\alpha}(x) \in K[x] \) is the minimal polynomial of \( \alpha \).
This assumption is not restrictive at all. Indeed if \( K \) has characteristic zero every finite extension \( K \hookrightarrow L \) is separable because \( K \) is perfect.
If \( K \) has characteristic \( p > 0 \) then for every finite field extension \( K \hookrightarrow L \) there exists a unique intermediate extension \( K \hookrightarrow E \hookrightarrow L \) such that \( K \hookrightarrow E \) is separable and \( E \hookrightarrow L \) is purely inseparable, i.e. for every \( \alpha \in L \) there exists \( n \in \mathbb{N} \) such that \( \alpha^{p^n} \in K \) (for a proof of this statement see Lemma 9.14.6 of the Stacks Project). It is clear now from the definition of a purely inseparable extension \( E \hookrightarrow L \) that every absolute value \( \psi \colon E \to \mathbb{R}_{\geq 0} \) extends uniquely to an absolute value \( \xi \colon L \to \mathbb{R}_{\geq 0} \) simply by setting \( \xi(\alpha) := (\psi(\alpha^{p^n}))^{p^{- n}} \) where \( n \in \mathbb{N} \) is such that \( \alpha^{p^n} \in E \).
We can thus assume without further hesitation that our finite extension \( K \hookrightarrow L \) is separable. Recall that in this case the primitive element theorem tells us that \( L = K(\alpha) \) for some \( \alpha \in L \). Thus we can reduce to the case of simple extensions in the following theorem.
Theorem 4 Let \( (K,\phi) \) be a valued field and let \( L = K(\alpha) \) be a finite simple extension of fields, and assume that the minimal polynomial \( f_{\alpha}(x) \in K[x] \) is separable. Then we have a bijection \[ \left\{ \psi \, \colon L \to \mathbb{R}_{\geq 0} \, \mid \, \psi \mid \phi \right\} \leftrightarrow \{ g_1(x), \dots, g_r(x) \} \] where \( \psi \mid \phi \) means that \( \psi \) extends \( \phi \) and \( \{ g_1, \dots, g_r \} \subseteq K_{\phi}[x] \) are the irreducible factors of the polynomial \( f_{\alpha}(x) \) over the completion \( K_{\phi} \) of \( K \) with respect to \( \phi \). In particular \( \phi \) can be extended to \( L \) in at least one way and at most \( [L \colon K] \)-ways and we have an isomorphism \[ K_{\phi} \otimes_{K} L \cong \prod_{\psi \mid \phi} L_{\psi} \] as \( K_{\phi} \)-algebras.
Proof Observe first of all that since \( f_{\alpha}(x) \) is separable it has only simple factors over \( K_{\phi} \), i.e. \( f_{\alpha}(x) = g_1(x) \cdots g_r(x) \in K_{\phi}[x] \) for some distinct, monic, irreducible polynomials \( g_1, \dots, g_r \in K_{\phi}[x] \). Recall now that \( L \cong K[x]/(f_{\alpha}(x)) \) (see this answer on Math StackExchange) and thus we have an isomorphism \[ K_{\phi} \otimes_{K} L \cong K_{\phi} \otimes_{K} \frac{K[x]}{(f_{\alpha}(x))} \cong \frac{K_{\phi}[x]}{(f_{\alpha}(x))} \cong \prod_{j = 1}^r \frac{K_{\phi}[x]}{(g_j(x))} \qquad \left( \dagger \right) \] as one sees applying Corollary 2.24 of these notes by Keith Conrad and Chinese remainder's theorem (see Lemma 10.14.4 of the Stacks Project).
 Recall now that \( K_{\phi}[x]/(g_j(x)) \) is a field for every \( j \in \{ 1,\dots,r\} \) because \( g_j(x) \in K_{\phi}[x] \) is irreducible (see Proposition 5.21 of these notes by Patrick Morandi). Moreover, this is a finite extension of the complete field \( (K_{\phi},\Phi) \) and thus, by Theorem 1 there exists a unique absolute value \( \Psi \colon K_{\phi}[x]/(g_j(x)) \to \mathbb{R}_{\geq 0} \) which extends \( \Phi \). Now, if we compose the canonical map \( L \to K_{\phi} \otimes_K L \) defined as \( x \mapsto 1 \otimes x \) with the isomorphism \( \left( \dagger \right) \) and with the projection \( \prod_{i = 1}^r K_{\phi}[x]/(g_i(x)) \twoheadrightarrow K_{\phi}[x]/(g_j(x)) \) we see that \( K_{\phi}[x]/(g_j(x)) \) is also a (very possibly infinite) extension of \( L \). Thus we can restrict the absolute value \( \Psi \) to an absolute value \( \psi \colon L \to \mathbb{R}_{\geq 0} \) and it is easy to see that \( \psi \) extends \( \phi \) because the diagram on the right is commutative. Thus we have constructed a map \[ F \colon \{ g_1(x), \dots, g_r(x) \} \to \{ \psi \, \colon L \to \mathbb{R}_{\geq 0} \, \mid \, \psi \mid \phi \} \] which associates to every irreducible factor of \( f_{\alpha}(x) \in K_{\phi}[x] \) an extension of the absolute value \( \phi \). In particular we have seen that every absolute value can be extended in at least one way.
Recall now that \( K_{\phi}[x]/(g_j(x)) \) is a field for every \( j \in \{ 1,\dots,r\} \) because \( g_j(x) \in K_{\phi}[x] \) is irreducible (see Proposition 5.21 of these notes by Patrick Morandi). Moreover, this is a finite extension of the complete field \( (K_{\phi},\Phi) \) and thus, by Theorem 1 there exists a unique absolute value \( \Psi \colon K_{\phi}[x]/(g_j(x)) \to \mathbb{R}_{\geq 0} \) which extends \( \Phi \). Now, if we compose the canonical map \( L \to K_{\phi} \otimes_K L \) defined as \( x \mapsto 1 \otimes x \) with the isomorphism \( \left( \dagger \right) \) and with the projection \( \prod_{i = 1}^r K_{\phi}[x]/(g_i(x)) \twoheadrightarrow K_{\phi}[x]/(g_j(x)) \) we see that \( K_{\phi}[x]/(g_j(x)) \) is also a (very possibly infinite) extension of \( L \). Thus we can restrict the absolute value \( \Psi \) to an absolute value \( \psi \colon L \to \mathbb{R}_{\geq 0} \) and it is easy to see that \( \psi \) extends \( \phi \) because the diagram on the right is commutative. Thus we have constructed a map \[ F \colon \{ g_1(x), \dots, g_r(x) \} \to \{ \psi \, \colon L \to \mathbb{R}_{\geq 0} \, \mid \, \psi \mid \phi \} \] which associates to every irreducible factor of \( f_{\alpha}(x) \in K_{\phi}[x] \) an extension of the absolute value \( \phi \). In particular we have seen that every absolute value can be extended in at least one way.
Suppose now that \( \psi \colon L \to \mathbb{R}_{\geq 0} \) is an absolute value extending \( \phi \). Then we know already from the fourth lecture that the completion \( L_{\psi} \) is an extension of \( L \) (by definition) and of \( K_{\phi} \) (by the universal property). Thus we can use the fact that the tensor product of algebras over a ring is a pushout (see page 27 of the same notes by Keith Conrad) to get a map \( K_{\phi} \otimes_K L \to L_{\psi} \). Observe that the image of this map is dense in \( L_{\psi} \) because it contains \( L \) and it is closed in \( L_{\psi} \) because it is a \( K_{\phi} \)-subspace of \( L_{\psi} \) and \( L_{\psi} \) is finite dimensional by Exercise 5, and thus we can apply Exercise 15 of the previous lecture. Thus the map \( K_{\phi} \otimes_K L \to L_{\psi} \) is surjective. We can use now Exercise 6 and the isomorphism \( K_{\phi} \otimes_{K} L \cong \prod_{i = 1}^r K_{\phi}[x]/(g_i(x)) \) to see that the surjective map \( K_{\phi} \otimes_K L \to L_{\psi} \) factors through a projection \( \prod_{i = 1}^r K_{\phi}[x]/(g_i(x)) \twoheadrightarrow K_{\phi}[x]/(g_j(x)) \) for some \( j \in \{ 1,\dots,r\} \). In particular the induced map \( K_{\phi}[x]/(g_j(x)) \to L_{\psi} \) is an isomorphism of fields. This construction gives us another map \[ G \colon \{ \psi \, \colon L \to \mathbb{R}_{\geq 0} \, \mid \, \psi \mid \phi \} \to \{ g_1(x), \dots, g_r(x) \} \] and it is not difficult to see that this is the inverse to the map defined in the previous paragraph.
Indeed to prove that \( G \circ F \) is the identity we only need to observe that \( K_{\phi}[x]/(g_i(x)) \cong K_{\phi}[x]/(g_j(x)) \) if and only if \( i = j \). To prove that \( F \circ G \) is the identity let \( \psi \) be an absolute value extending \( \phi \) and let \( \psi' := F(G(\psi)) \). Then we have that \( L_{\psi'} \cong K_{\phi}[x]/(g_j(x)) \) where \( g_{j}(x) = G(\psi) \). But then \( L_{\psi'} \cong L_{\psi} \) and this implies that \( \psi = \psi' \). Q.E.D.
Exercise 5 Let \( (K,\phi) \hookrightarrow (L,\psi) \) be a finite extension of valued fields. Prove that \( (K_{\phi},\Phi) \hookrightarrow (L_{\psi},\Psi) \) is also a finite extension of degree less or equal to \( [L \colon K] \). (Hint: if \( \alpha \in L_{\psi} \) then it is a limit of a sequence of elements \( \{ \alpha_k \} \subseteq L \) and each one of them satisfies an equation of degree (at most) \( [L \colon K] \). Prove that \( \alpha \) satisfies the equation obtained as a limit of these equations and conclude).
Exercise 6 Let \( R \subseteq \prod_{i \in I} A_i \) be a subring of a product or rings. Prove that \( R \) is an integral domain if and only if \( R \subseteq A_i \) for some \( i \in I \) and \( A_i \) is itself an integral domain. (This is a very easy exercise).
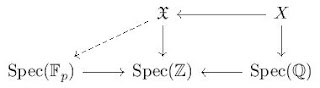
Example 7 Let \( K \subseteq L \) be an extension of number fields, and let \( \phi \colon K \to \mathbb{R}_{\geq 0} \) be a non-Archimedean absolute value. We know already that \( \phi \) is equivalent to \( \lvert \cdot \rvert_{\mathfrak{p}} \) for some prime ideal \( \mathfrak{p} \subseteq \mathcal{O}_K \) (see Theorem 7 of the third lecture). Let now \( \psi \colon L \to \mathbb{R}_{\geq 0} \) be an absolute value extending \( \phi \), and suppose that \( L \) is equivalent to \( \lvert \cdot \rvert_{\mathfrak{P}} \) for some \( \mathfrak{P} \subseteq \mathcal{O}_L \). Then for every \( \alpha \in \mathcal{O}_K \) we have that \( \alpha \in \mathfrak{p} \) if and only if \( \lvert \alpha \rvert_{\mathfrak{p}} < 1 \), and this is true if and only if \( \lvert \alpha \rvert_{\mathfrak{P}} < 1 \), which holds if and only if \( \alpha \in \mathfrak{P} \cap \mathcal{O}_K \). Thus we have proved that \( \mathfrak{p} = \mathfrak{P} \cap \mathcal{O}_K \), i.e. that \( \mathfrak{p} \) is the contraction of \( \mathfrak{P} \) to \( \mathcal{O}_K \). We see in this way that extensions of absolute values correspond (in the case of number fields) to extensions of prime ideals.
Definition 8 Let \( (K,\phi) \hookrightarrow (L,\psi) \) be an extension of valued fields. We define the inertia index \( e(L \mid K) = e(\psi \mid \phi) \) as the index of the subgroup \( \phi(K^{\times}) \leq \psi(L^{\times}) \) and the ramification index \( f(L \mid K) = f(\psi \mid \phi) \) as the degree of the extension of residue fields \( \kappa_{\phi} \subseteq \kappa_{\psi} \) (see the diagram on the right).
Definition 9 We say that an extension of valued fields \( (K,\phi) \hookrightarrow (L,\psi) \) is:
Theorem 10 Let \( (K,\phi) \) be a non-Archimedean, valued field, and let \( K \subseteq L \) be a finite, separable extension of fields. Then we have the inequality \[ \sum_{\psi \mid \phi} e(\psi \mid \phi) f(\psi \mid \phi) \leq [L \colon K] \] and the equality holds if \( \phi \) is a discrete absolute value.
Proof Observe first of all that the dimension of \( K_{\phi} \otimes_K L \) as a \( K_{\phi} \)-vector space is equal to the dimension of \( L \) as a \( K \)-vector space, i.e. to \( [L \colon K] \). Recall from Theorem 4 that we have an isomorphism \( K_{\phi} \otimes_K L \cong \prod_{\psi \mid \phi} L_{\psi} \) and observe that the dimension of the vector space on the right is equal to \( \sum_{\psi \mid \phi} [L_{\psi} \colon K_{\phi}] \). Thus we have that \( [L \colon K] = \sum_{\psi \mid \phi} [L_{\psi} \colon K_{\phi}] \) and we would have proved the theorem if we knew that \( [L_{\psi} \colon K_{\phi}] \geq e(\psi \mid \phi) f(\psi \mid \phi) \) for every \( \psi \mid \phi \). Thanks to Exercise 2 of the ninth lecture we know that \( e(\psi \mid \phi) = e(\Psi \mid \Phi) \) and \( f(\psi \mid \phi) = f(\Psi \mid \Phi) \), where \( \Phi \) and \( \Psi \) are the extensions of \( \phi \) and \( \psi \) to the completions \( K_{\phi} \) and \( L_{\psi} \). To prove the theorem it is hence sufficient to prove it for complete fields.
Thus from here until the end of the proof we will assume that \( (K,\phi) \) is complete and that \( \psi \colon L \to \mathbb{R}_{\geq 0} \) is the unique extension of \( \phi \) to \( L \). In this case we simply have to prove that \( e(\psi \mid \phi) f(\psi \mid \phi) \leq [L \colon K] \), because the extension is unique. Let \( R \subseteq A_{\psi}^{\times} \) be a set of elements whose reduction modulo \(\mathfrak{m}_{\psi} \) becomes a \( \kappa_{\phi} \)-basis for \( \kappa_{\psi} \) and let \( S \subseteq L^{\times} \) be a set of elements whose image under \( \psi \) is a set of coset representatives for the subgroup \( \phi(K^{\times}) \subseteq \psi(L^{\times}) \).
Suppose now that \[ \sum_{r \in R, \, s \in s} a_{r,s} r s = 0 \] for some \( a_{r,s} \in K \) which are all zero except from a finite number of them. Then if \( \alpha_s := \sum_{r \in R} a_{r,s} r \in L \) we have that \( \psi(\alpha_s) \leq \max_r \phi(a_{r,s}) \) by the ultrametric inequality and the fact that \( R \subseteq A_{\psi} \). Thus we have that \( a_{r_s,s}^{-1} \alpha_s \in A_{\psi}^{\times} \) for some \( r_s \in R \) (the one such that \( \phi(a_{r_s,s}) \geq \phi(a_{r,s}) \) for all \( r \in R \) ). Thus if \( 0 \neq \psi(\alpha_{s_1} s_1) = \psi(\alpha_{s_2} s_2) \) for some \( s_1, s_2 \in S \) we have that \( s_1 = s_2 \). Indeed by the definition of \( S \) this is true if and only if \( \psi(s_1 s_2^{-1}) \in \phi(K^{\times}) \) and we have that \[ \psi(s_1 s_2^{-1}) = \psi(\alpha_{s_2} \alpha_{s_1}^{-1}) = \psi(a_{r_{s_2},s_2}^{-1} \, \alpha_{s_2}) \psi(a_{r_{s_1},s_1} \alpha_{s_1}^{-1}) \phi(a_{r_{s_2},s_2} a_{r_{s_1},s_1}^{-1}) = \phi(a_{r_{s_2},s_2} a_{r_{s_1},s_1}^{-1}) \in \phi(K^{\times}) \] which implies that \( s_1 = s_2 \) and thus that all the elements \( \alpha_s s \) have either zero or different absolute values. This finally implies that \( a_{r,s} = 0 \) for all \( r \in R \) and \( s \in S \) because \[ 0 = \psi\left( \sum_{r \in R, \, s \in s} a_{r,s} r s \right) = \psi\left( \sum_{s \in S} \alpha_s s \right) = \max_{s \in S} \psi(\alpha_s s) \]
which implies that \( \alpha_s = 0 \) for all \( s \in S \) and thus that \( a_{r,s} = 0 \) for all \( r \in R \) and \( s \in S \).
Thus we have shown that the set \( \{ r s \mid r \in R, \, s \in S \} \subseteq L \) is a set of elements which are linearly independent over \( K \). This proves that \( R \) and \( S \) are finite because \( K \subseteq L \) is finite and that \( \# R \cdot \# S = f(\psi \mid \phi) e(\psi \mid \phi) \leq [L \colon K] \).
Suppose finally that \( \phi(K^{\times}) \leq \mathbb{R}_{> 0} \) is a discrete subgroup. Then \( \psi(L^{\times}) \) is also a discrete subgroup (because \( \phi(K^{\times}) \) is a subgroup of finite index inside \( \psi(L^{\times}) \) ) and we know (see Lemma 2 of the third lecture) that \( A_{\phi} \) and \( A_{\psi} \) are discrete valuation rings. Let \( \pi \in A_{\phi} \) and \( \Pi \in A_{\psi} \) be uniformizers, and let \( T_{\phi} \subseteq A_{\phi} \) be a set of representatives for the quotitent \( A_{\phi}/\mathfrak{m}_{\phi} \) which contains zero. Then the set \[ T_{\psi} := \sum_{r \in R} T \cdot r = \left\{ \sum_{r \in R} t_r \, r \mid t_r \in T_{\phi} \right\} \] is a set of representatives for the quotient \( A_{\psi}/\mathfrak{m}_{\psi} \) which contains zero, because by definition \( R \subseteq A_{\psi}^{\times} \) was a set of elements whose reduction modulo \( \mathfrak{m}_{\psi} \) gave us a basis for the extension of fields \( A_{\phi}/\mathfrak{m}_{\phi} \subseteq A_{\psi}/\mathfrak{m}_{\psi} \).
To conclude we only need to observe that \( \Pi^{e(\psi \mid \phi)} = u \pi \) for some \( u \in A_{\phi}^{\times} \) because \( \phi(\pi) \) and \( \psi(\Pi) \) generate \( \phi(K^{\times}) \) and \( \psi(L^{\times}) \) respectively. Thus we have that \( \mathfrak{m}_{\psi}^n \) is generated by \( \Pi^n = \pi^i \Pi^j \) with \( 0 \leq j < e(\psi \colon \phi) \) and we can apply Proposition 8 of the ninth lecture to see that every \( \alpha \in A_{\psi} \) can be written as \( \alpha = \sum_{i,j} t_{i,j} \pi^i \Pi^j \) for some \( t_{i,j} \in T_{\psi} \). Thus using the definition of \( T_{\psi} \) we know that every element \( \alpha \in A_{\psi} \) can be written as \[ \alpha = \sum_{r \in R} \sum_{j = 1}^{e(\psi \mid \phi)} \left( \sum_{k = 0}^{+\infty} t_{i,j,k} \pi^k \right) r \Pi^j \] for some \( t_{i,j,k} \in T_{\phi} \). This proves that \[ A_{\psi} = \bigoplus_{r \in R} \bigoplus_{j = 1}^{e(\psi \mid \phi)} A_{\phi} \, r \, \Pi^j \] and thus that the set \( \{ r \, \Pi^j \mid r \in R, \, j \in \{ 1, \dots, e(\psi \mid \phi) \} \, \} \) is a \(K\)-basis for \( L \), which implies that \( f(\psi \mid \phi) e(\psi \mid \phi) = [L \colon K] \) as we wanted to prove. Q.E.D.
Exercise 11 Let \( K \subseteq L \) be an extension of number fields, let \( \mathfrak{P} \subseteq \mathcal{O}_L \) be a prime ideal and let \( \mathfrak{p} := \mathfrak{P} \cap \mathcal{O}_K \). Prove that \( e(\lvert \cdot \rvert_{\mathfrak{P}}, \lvert \cdot \rvert_{\mathfrak{p}}) \) is the maximum of all \( n \in \mathbb{N} \) such that \( \mathfrak{P}^n \mid \mathfrak{p} \mathcal{O}_L \). (Hint: recall what we said in the proof of the previous theorem about the uniformizers...).
In the previous lecture we have seen two useful applications of completeness: Hensel's lemma, which allows us to solve equations in complete fields by solving them in their residue fields, and a characterization of norms on finite dimensional vector spaces over complete fields.
The aim of this lecture is to use the second result as a starting point to study the theory of the extensions of absolute values to an algebraic extension. We have already seen in the second lecture that if we have a field extension \( K \hookrightarrow L \) and an absolute value \( \psi \colon L \to \mathbb{R}_{\geq 0} \) we can restrict it to an absolute value \( \phi \colon K \to \mathbb{R}_{\geq 0} \).
Suppose now that we have an absolute value \( \phi \colon K \to \mathbb{R}_{\geq 0} \). Can we extend it to an absolute value \( \psi \colon L \to \mathbb{R}_{\geq 0} \)? And if we have two absolute values \( \psi_1, \psi_2 \colon L \to \mathbb{R}_{\geq 0} \) which restrict to the same absolute value on \( K \), how are they related?
Extending complete absolute values
We will start to answer to this question from the complete case. Indeed, we have already seen an example of extension of an absolute value from a complete field in the fourth lecture, where we proved in Lemma 10 that if \( (K,\phi) \) is a complete valued field and \( L = K(i) \) is a quadratic extension of \( K \) with \( i^2 + 1 = 0 \) then \( L \) is complete with respect to the absolute value \( \psi \colon L \to \mathbb{R}_{\geq 0} \) defined by \( \psi(x + i y) = \sqrt{\phi(x)^2 + \phi(y)^2} \). To be honest, we didn't prove completely that \( \psi \) was an absolute value, because we didn't prove that it satisfied the triangle inequality.It is now time to remedy to this lack and to generalize this to arbitrary finite extensions of complete fields. To do so we recall that if \( K \hookrightarrow L \) is a finite extension of fields we can define the field norm \begin{align} \operatorname{N}_{L/K} \colon L &\to K \\ \alpha &\mapsto \det_K(\mu_{\alpha}) \end{align} where \( \mu_{\alpha} \colon L \to L \) is the \( K \)-linear map defined by \( \mu_{\alpha}(x) := \alpha \, x \). Observe that the multiplicativity of the determinant immediately implies that the norm is multiplicative, i.e. \( \operatorname{N}_{L/K}(\alpha \beta) = \operatorname{N}_{L/K}(\alpha) \, \operatorname{N}_{L/K}(\beta) \) for all \( \alpha,\beta \in L \).
Theorem 1 Let \( (K,\phi) \) be a complete valued field and let \( K \hookrightarrow L \) be a finite extension of degree \( d = [L \colon K] \). Then the map \( \psi \colon L \to \mathbb{R}_{\geq 0} \) defined by \( \psi(x) := \sqrt[d]{\phi(\operatorname{N}_{L/K}(x))} \) is the unique extension of the absolute value \( \phi \) to \( L \). Moreover, \( L \) is complete with respect to \( \phi \).
Proof If \( d = 1 \) there is nothing to prove. Moreover if \( d \neq 1 \) and \( K \) is Archimedean then Theorem 16 of the fourth lecture tells us that \( d = 2 \), \( K \cong \mathbb{R} \) and \( L \cong \mathbb{C} \) and in this case this theorem is equivalent to Lemma 10 of the fourth lecture.
Suppose hence that \( (K,\phi) \) is non-Archimedean and \( d \geq 2 \). It is trivial to observe that \( \psi \) satisfies the first two axioms of Definition 1 of the second lecture. We want to check now that \( \psi(x + y) \leq \max(\psi(x),\psi(y)) \) and we know from Exercise 17 of the second lecture that this is equivalent to check that \( \psi(1 + t) \leq 1 \) for all \( t \in L \) such that \( \psi(t) \leq 1 \). Observe that for every \( x \in L \) we have that \( \operatorname{N}_{L/K}(x) = f_x(0)^{m_x} \) where \( f_x(T) \in K[T] \) is the minimal polynomial of \( x \) and \( m_x \in \mathbb{N} \). Observe moreover that \( f_{1 + x}(T) = f_x(T - 1) \) which implies that \( \psi(1 + t) \leq 1 \) if and only if \( \phi(f_t(- 1)) \leq 1 \). This would automatically follow if \( f_t(T) \in A_{\phi}[T] \).
Thus let \( t \in L \) be any element with \( \psi(t) \leq 1 \). We have that \( f_t(0) \in A_{\phi} \) because \( \psi(t) \leq 1 \) is equivalent to \( \phi(f_t(0)) \leq 1 \) and we want to prove that \( f_t \in A_{\phi} \). This follows from Hensel's lemma (see Theorem 5 of the previous lecture). Indeed if \( f_t(T) \notin A_{\phi}[T] \) then we can "clear denominators", i.e. we can find \( \alpha \in K^{\times} \) with \( \phi(\alpha) < 1 \) such that \( \alpha f_t(T) \in A_{\phi}[T] \). Observe that since \( f \) is monic and \( \phi(f_t(0)) \leq 1 \) if we write \( \alpha f_t(T) = \sum_{j = 0}^n c_j T^j \) we have that \( c_0, c_n \in \mathfrak{m}_{\phi} \). This is equivalent to say that \[ 0 < \max\{ k \, \colon \, T^k \mid \overline{\alpha f_t} \in \kappa_{\phi}[T] \} < \deg(f_t) \] and thus by Hensel's lemma there exists a polynomial \( g(T) \in A_{\phi}[T] \) such that \( \deg(g) < \deg(f_t) \) and \( g \mid f_t \). But this is absurd because the minimal polynomial \( f_t \) is irreducible.
To conclude we only have to observe that \( \psi \) is a norm on \( L \) considered as a vector space over \( K \), in the sense of Definition 8 of the previous lecture. Thus we only have to apply Theorem 14 of the previous lecture to see that \( L \) is complete with respect to \( \psi \) and that \( \psi \) is unique up to equivalence. Since \( \psi \) extends \( \phi \) we also see that \( \psi \) is unique. Q.E.D.
The proof of the previous theorem tells us that the ring \( A_{\psi} \) associated to a non-Archimedean, complete absolute value \( \psi \colon L \to \mathbb{R}_{\geq 0} \) which extends \( \phi \colon K \to \mathbb{R}_{\geq 0} \) is strongly related to \( A_{\phi} \). More precisely for every \( \alpha \in L \) we have that \( \alpha \in A_{\psi} \) if and only if \( f_{\alpha}(x) \in A_{\phi}[x] \). This property is so important that it deserves a name.
Definition 2 Let \( A \subseteq B \) be an extension of rings. Then the integral closure of \( A \) in \( B \) is the ring \( \overline{A} \subseteq B \) of all elements \( b \in B \) such that \( f(b) = 0 \) for some monic polynomial \( f(x) = x^n + a_{n - 1} x^{n - 1} + \dots + a_0 \in A[x] \).
Corollary 3 Let \( (K,\phi) \) be a non-Archimedean, complete valued field, let \( K \hookrightarrow L \) be a finite extension and let \( \psi \colon L \to \mathbb{R}_{\geq 0} \) be an absolute value extending \( \phi \). Then the ring \( A_{\psi} \subseteq L \) is the integral closure of \( A_{\phi} \) inside \( L \).
Extending absolute values
We deal now with the general problem of extending an absolute value \( \phi \colon K \to \mathbb{R}_{\geq 0} \) to a finite extension \( K \hookrightarrow L \).To proceed we will need to assume that this extension is separable, i.e. that for every \( \alpha \in L \) we have that \( f_{\alpha}'(x) \neq 0 \), where \( f_{\alpha}(x) \in K[x] \) is the minimal polynomial of \( \alpha \).
This assumption is not restrictive at all. Indeed if \( K \) has characteristic zero every finite extension \( K \hookrightarrow L \) is separable because \( K \) is perfect.
If \( K \) has characteristic \( p > 0 \) then for every finite field extension \( K \hookrightarrow L \) there exists a unique intermediate extension \( K \hookrightarrow E \hookrightarrow L \) such that \( K \hookrightarrow E \) is separable and \( E \hookrightarrow L \) is purely inseparable, i.e. for every \( \alpha \in L \) there exists \( n \in \mathbb{N} \) such that \( \alpha^{p^n} \in K \) (for a proof of this statement see Lemma 9.14.6 of the Stacks Project). It is clear now from the definition of a purely inseparable extension \( E \hookrightarrow L \) that every absolute value \( \psi \colon E \to \mathbb{R}_{\geq 0} \) extends uniquely to an absolute value \( \xi \colon L \to \mathbb{R}_{\geq 0} \) simply by setting \( \xi(\alpha) := (\psi(\alpha^{p^n}))^{p^{- n}} \) where \( n \in \mathbb{N} \) is such that \( \alpha^{p^n} \in E \).
We can thus assume without further hesitation that our finite extension \( K \hookrightarrow L \) is separable. Recall that in this case the primitive element theorem tells us that \( L = K(\alpha) \) for some \( \alpha \in L \). Thus we can reduce to the case of simple extensions in the following theorem.
Theorem 4 Let \( (K,\phi) \) be a valued field and let \( L = K(\alpha) \) be a finite simple extension of fields, and assume that the minimal polynomial \( f_{\alpha}(x) \in K[x] \) is separable. Then we have a bijection \[ \left\{ \psi \, \colon L \to \mathbb{R}_{\geq 0} \, \mid \, \psi \mid \phi \right\} \leftrightarrow \{ g_1(x), \dots, g_r(x) \} \] where \( \psi \mid \phi \) means that \( \psi \) extends \( \phi \) and \( \{ g_1, \dots, g_r \} \subseteq K_{\phi}[x] \) are the irreducible factors of the polynomial \( f_{\alpha}(x) \) over the completion \( K_{\phi} \) of \( K \) with respect to \( \phi \). In particular \( \phi \) can be extended to \( L \) in at least one way and at most \( [L \colon K] \)-ways and we have an isomorphism \[ K_{\phi} \otimes_{K} L \cong \prod_{\psi \mid \phi} L_{\psi} \] as \( K_{\phi} \)-algebras.
Proof Observe first of all that since \( f_{\alpha}(x) \) is separable it has only simple factors over \( K_{\phi} \), i.e. \( f_{\alpha}(x) = g_1(x) \cdots g_r(x) \in K_{\phi}[x] \) for some distinct, monic, irreducible polynomials \( g_1, \dots, g_r \in K_{\phi}[x] \). Recall now that \( L \cong K[x]/(f_{\alpha}(x)) \) (see this answer on Math StackExchange) and thus we have an isomorphism \[ K_{\phi} \otimes_{K} L \cong K_{\phi} \otimes_{K} \frac{K[x]}{(f_{\alpha}(x))} \cong \frac{K_{\phi}[x]}{(f_{\alpha}(x))} \cong \prod_{j = 1}^r \frac{K_{\phi}[x]}{(g_j(x))} \qquad \left( \dagger \right) \] as one sees applying Corollary 2.24 of these notes by Keith Conrad and Chinese remainder's theorem (see Lemma 10.14.4 of the Stacks Project).
 Recall now that \( K_{\phi}[x]/(g_j(x)) \) is a field for every \( j \in \{ 1,\dots,r\} \) because \( g_j(x) \in K_{\phi}[x] \) is irreducible (see Proposition 5.21 of these notes by Patrick Morandi). Moreover, this is a finite extension of the complete field \( (K_{\phi},\Phi) \) and thus, by Theorem 1 there exists a unique absolute value \( \Psi \colon K_{\phi}[x]/(g_j(x)) \to \mathbb{R}_{\geq 0} \) which extends \( \Phi \). Now, if we compose the canonical map \( L \to K_{\phi} \otimes_K L \) defined as \( x \mapsto 1 \otimes x \) with the isomorphism \( \left( \dagger \right) \) and with the projection \( \prod_{i = 1}^r K_{\phi}[x]/(g_i(x)) \twoheadrightarrow K_{\phi}[x]/(g_j(x)) \) we see that \( K_{\phi}[x]/(g_j(x)) \) is also a (very possibly infinite) extension of \( L \). Thus we can restrict the absolute value \( \Psi \) to an absolute value \( \psi \colon L \to \mathbb{R}_{\geq 0} \) and it is easy to see that \( \psi \) extends \( \phi \) because the diagram on the right is commutative. Thus we have constructed a map \[ F \colon \{ g_1(x), \dots, g_r(x) \} \to \{ \psi \, \colon L \to \mathbb{R}_{\geq 0} \, \mid \, \psi \mid \phi \} \] which associates to every irreducible factor of \( f_{\alpha}(x) \in K_{\phi}[x] \) an extension of the absolute value \( \phi \). In particular we have seen that every absolute value can be extended in at least one way.
Recall now that \( K_{\phi}[x]/(g_j(x)) \) is a field for every \( j \in \{ 1,\dots,r\} \) because \( g_j(x) \in K_{\phi}[x] \) is irreducible (see Proposition 5.21 of these notes by Patrick Morandi). Moreover, this is a finite extension of the complete field \( (K_{\phi},\Phi) \) and thus, by Theorem 1 there exists a unique absolute value \( \Psi \colon K_{\phi}[x]/(g_j(x)) \to \mathbb{R}_{\geq 0} \) which extends \( \Phi \). Now, if we compose the canonical map \( L \to K_{\phi} \otimes_K L \) defined as \( x \mapsto 1 \otimes x \) with the isomorphism \( \left( \dagger \right) \) and with the projection \( \prod_{i = 1}^r K_{\phi}[x]/(g_i(x)) \twoheadrightarrow K_{\phi}[x]/(g_j(x)) \) we see that \( K_{\phi}[x]/(g_j(x)) \) is also a (very possibly infinite) extension of \( L \). Thus we can restrict the absolute value \( \Psi \) to an absolute value \( \psi \colon L \to \mathbb{R}_{\geq 0} \) and it is easy to see that \( \psi \) extends \( \phi \) because the diagram on the right is commutative. Thus we have constructed a map \[ F \colon \{ g_1(x), \dots, g_r(x) \} \to \{ \psi \, \colon L \to \mathbb{R}_{\geq 0} \, \mid \, \psi \mid \phi \} \] which associates to every irreducible factor of \( f_{\alpha}(x) \in K_{\phi}[x] \) an extension of the absolute value \( \phi \). In particular we have seen that every absolute value can be extended in at least one way.Suppose now that \( \psi \colon L \to \mathbb{R}_{\geq 0} \) is an absolute value extending \( \phi \). Then we know already from the fourth lecture that the completion \( L_{\psi} \) is an extension of \( L \) (by definition) and of \( K_{\phi} \) (by the universal property). Thus we can use the fact that the tensor product of algebras over a ring is a pushout (see page 27 of the same notes by Keith Conrad) to get a map \( K_{\phi} \otimes_K L \to L_{\psi} \). Observe that the image of this map is dense in \( L_{\psi} \) because it contains \( L \) and it is closed in \( L_{\psi} \) because it is a \( K_{\phi} \)-subspace of \( L_{\psi} \) and \( L_{\psi} \) is finite dimensional by Exercise 5, and thus we can apply Exercise 15 of the previous lecture. Thus the map \( K_{\phi} \otimes_K L \to L_{\psi} \) is surjective. We can use now Exercise 6 and the isomorphism \( K_{\phi} \otimes_{K} L \cong \prod_{i = 1}^r K_{\phi}[x]/(g_i(x)) \) to see that the surjective map \( K_{\phi} \otimes_K L \to L_{\psi} \) factors through a projection \( \prod_{i = 1}^r K_{\phi}[x]/(g_i(x)) \twoheadrightarrow K_{\phi}[x]/(g_j(x)) \) for some \( j \in \{ 1,\dots,r\} \). In particular the induced map \( K_{\phi}[x]/(g_j(x)) \to L_{\psi} \) is an isomorphism of fields. This construction gives us another map \[ G \colon \{ \psi \, \colon L \to \mathbb{R}_{\geq 0} \, \mid \, \psi \mid \phi \} \to \{ g_1(x), \dots, g_r(x) \} \] and it is not difficult to see that this is the inverse to the map defined in the previous paragraph.
Indeed to prove that \( G \circ F \) is the identity we only need to observe that \( K_{\phi}[x]/(g_i(x)) \cong K_{\phi}[x]/(g_j(x)) \) if and only if \( i = j \). To prove that \( F \circ G \) is the identity let \( \psi \) be an absolute value extending \( \phi \) and let \( \psi' := F(G(\psi)) \). Then we have that \( L_{\psi'} \cong K_{\phi}[x]/(g_j(x)) \) where \( g_{j}(x) = G(\psi) \). But then \( L_{\psi'} \cong L_{\psi} \) and this implies that \( \psi = \psi' \). Q.E.D.
Exercise 5 Let \( (K,\phi) \hookrightarrow (L,\psi) \) be a finite extension of valued fields. Prove that \( (K_{\phi},\Phi) \hookrightarrow (L_{\psi},\Psi) \) is also a finite extension of degree less or equal to \( [L \colon K] \). (Hint: if \( \alpha \in L_{\psi} \) then it is a limit of a sequence of elements \( \{ \alpha_k \} \subseteq L \) and each one of them satisfies an equation of degree (at most) \( [L \colon K] \). Prove that \( \alpha \) satisfies the equation obtained as a limit of these equations and conclude).
Exercise 6 Let \( R \subseteq \prod_{i \in I} A_i \) be a subring of a product or rings. Prove that \( R \) is an integral domain if and only if \( R \subseteq A_i \) for some \( i \in I \) and \( A_i \) is itself an integral domain. (This is a very easy exercise).
Example 7 Let \( K \subseteq L \) be an extension of number fields, and let \( \phi \colon K \to \mathbb{R}_{\geq 0} \) be a non-Archimedean absolute value. We know already that \( \phi \) is equivalent to \( \lvert \cdot \rvert_{\mathfrak{p}} \) for some prime ideal \( \mathfrak{p} \subseteq \mathcal{O}_K \) (see Theorem 7 of the third lecture). Let now \( \psi \colon L \to \mathbb{R}_{\geq 0} \) be an absolute value extending \( \phi \), and suppose that \( L \) is equivalent to \( \lvert \cdot \rvert_{\mathfrak{P}} \) for some \( \mathfrak{P} \subseteq \mathcal{O}_L \). Then for every \( \alpha \in \mathcal{O}_K \) we have that \( \alpha \in \mathfrak{p} \) if and only if \( \lvert \alpha \rvert_{\mathfrak{p}} < 1 \), and this is true if and only if \( \lvert \alpha \rvert_{\mathfrak{P}} < 1 \), which holds if and only if \( \alpha \in \mathfrak{P} \cap \mathcal{O}_K \). Thus we have proved that \( \mathfrak{p} = \mathfrak{P} \cap \mathcal{O}_K \), i.e. that \( \mathfrak{p} \) is the contraction of \( \mathfrak{P} \) to \( \mathcal{O}_K \). We see in this way that extensions of absolute values correspond (in the case of number fields) to extensions of prime ideals.
Ramification and inertia
We have just seen that every absolute value \( \phi \colon K \to \mathbb{R}_{\geq 0} \) on a field \( K \) admits a finite number of extensions to a finite extension \( L \supseteq K \). We would like now to understand the extension of valued fields \( (K,\phi) \hookrightarrow (L,\psi) \), and to do so we start by defining two important invariants of this extension.Definition 8 Let \( (K,\phi) \hookrightarrow (L,\psi) \) be an extension of valued fields. We define the inertia index \( e(L \mid K) = e(\psi \mid \phi) \) as the index of the subgroup \( \phi(K^{\times}) \leq \psi(L^{\times}) \) and the ramification index \( f(L \mid K) = f(\psi \mid \phi) \) as the degree of the extension of residue fields \( \kappa_{\phi} \subseteq \kappa_{\psi} \) (see the diagram on the right).
Definition 9 We say that an extension of valued fields \( (K,\phi) \hookrightarrow (L,\psi) \) is:
- unramified if \( e(L \mid K) = 1 \) and the extension \( \kappa_{\phi} \subseteq \kappa_{\psi} \) is separable;
- totally ramified if \( f(L \mid K) = 1 \);
- tamely ramified if \( e(L \mid K) \) is relatively prime to the characteristic of \( \kappa_{\phi} \) and the extension \( \kappa_{\phi} \subseteq \kappa_{\psi} \) is separable.
Theorem 10 Let \( (K,\phi) \) be a non-Archimedean, valued field, and let \( K \subseteq L \) be a finite, separable extension of fields. Then we have the inequality \[ \sum_{\psi \mid \phi} e(\psi \mid \phi) f(\psi \mid \phi) \leq [L \colon K] \] and the equality holds if \( \phi \) is a discrete absolute value.
Proof Observe first of all that the dimension of \( K_{\phi} \otimes_K L \) as a \( K_{\phi} \)-vector space is equal to the dimension of \( L \) as a \( K \)-vector space, i.e. to \( [L \colon K] \). Recall from Theorem 4 that we have an isomorphism \( K_{\phi} \otimes_K L \cong \prod_{\psi \mid \phi} L_{\psi} \) and observe that the dimension of the vector space on the right is equal to \( \sum_{\psi \mid \phi} [L_{\psi} \colon K_{\phi}] \). Thus we have that \( [L \colon K] = \sum_{\psi \mid \phi} [L_{\psi} \colon K_{\phi}] \) and we would have proved the theorem if we knew that \( [L_{\psi} \colon K_{\phi}] \geq e(\psi \mid \phi) f(\psi \mid \phi) \) for every \( \psi \mid \phi \). Thanks to Exercise 2 of the ninth lecture we know that \( e(\psi \mid \phi) = e(\Psi \mid \Phi) \) and \( f(\psi \mid \phi) = f(\Psi \mid \Phi) \), where \( \Phi \) and \( \Psi \) are the extensions of \( \phi \) and \( \psi \) to the completions \( K_{\phi} \) and \( L_{\psi} \). To prove the theorem it is hence sufficient to prove it for complete fields.
Thus from here until the end of the proof we will assume that \( (K,\phi) \) is complete and that \( \psi \colon L \to \mathbb{R}_{\geq 0} \) is the unique extension of \( \phi \) to \( L \). In this case we simply have to prove that \( e(\psi \mid \phi) f(\psi \mid \phi) \leq [L \colon K] \), because the extension is unique. Let \( R \subseteq A_{\psi}^{\times} \) be a set of elements whose reduction modulo \(\mathfrak{m}_{\psi} \) becomes a \( \kappa_{\phi} \)-basis for \( \kappa_{\psi} \) and let \( S \subseteq L^{\times} \) be a set of elements whose image under \( \psi \) is a set of coset representatives for the subgroup \( \phi(K^{\times}) \subseteq \psi(L^{\times}) \).
Suppose now that \[ \sum_{r \in R, \, s \in s} a_{r,s} r s = 0 \] for some \( a_{r,s} \in K \) which are all zero except from a finite number of them. Then if \( \alpha_s := \sum_{r \in R} a_{r,s} r \in L \) we have that \( \psi(\alpha_s) \leq \max_r \phi(a_{r,s}) \) by the ultrametric inequality and the fact that \( R \subseteq A_{\psi} \). Thus we have that \( a_{r_s,s}^{-1} \alpha_s \in A_{\psi}^{\times} \) for some \( r_s \in R \) (the one such that \( \phi(a_{r_s,s}) \geq \phi(a_{r,s}) \) for all \( r \in R \) ). Thus if \( 0 \neq \psi(\alpha_{s_1} s_1) = \psi(\alpha_{s_2} s_2) \) for some \( s_1, s_2 \in S \) we have that \( s_1 = s_2 \). Indeed by the definition of \( S \) this is true if and only if \( \psi(s_1 s_2^{-1}) \in \phi(K^{\times}) \) and we have that \[ \psi(s_1 s_2^{-1}) = \psi(\alpha_{s_2} \alpha_{s_1}^{-1}) = \psi(a_{r_{s_2},s_2}^{-1} \, \alpha_{s_2}) \psi(a_{r_{s_1},s_1} \alpha_{s_1}^{-1}) \phi(a_{r_{s_2},s_2} a_{r_{s_1},s_1}^{-1}) = \phi(a_{r_{s_2},s_2} a_{r_{s_1},s_1}^{-1}) \in \phi(K^{\times}) \] which implies that \( s_1 = s_2 \) and thus that all the elements \( \alpha_s s \) have either zero or different absolute values. This finally implies that \( a_{r,s} = 0 \) for all \( r \in R \) and \( s \in S \) because \[ 0 = \psi\left( \sum_{r \in R, \, s \in s} a_{r,s} r s \right) = \psi\left( \sum_{s \in S} \alpha_s s \right) = \max_{s \in S} \psi(\alpha_s s) \]
which implies that \( \alpha_s = 0 \) for all \( s \in S \) and thus that \( a_{r,s} = 0 \) for all \( r \in R \) and \( s \in S \).
Thus we have shown that the set \( \{ r s \mid r \in R, \, s \in S \} \subseteq L \) is a set of elements which are linearly independent over \( K \). This proves that \( R \) and \( S \) are finite because \( K \subseteq L \) is finite and that \( \# R \cdot \# S = f(\psi \mid \phi) e(\psi \mid \phi) \leq [L \colon K] \).
Suppose finally that \( \phi(K^{\times}) \leq \mathbb{R}_{> 0} \) is a discrete subgroup. Then \( \psi(L^{\times}) \) is also a discrete subgroup (because \( \phi(K^{\times}) \) is a subgroup of finite index inside \( \psi(L^{\times}) \) ) and we know (see Lemma 2 of the third lecture) that \( A_{\phi} \) and \( A_{\psi} \) are discrete valuation rings. Let \( \pi \in A_{\phi} \) and \( \Pi \in A_{\psi} \) be uniformizers, and let \( T_{\phi} \subseteq A_{\phi} \) be a set of representatives for the quotitent \( A_{\phi}/\mathfrak{m}_{\phi} \) which contains zero. Then the set \[ T_{\psi} := \sum_{r \in R} T \cdot r = \left\{ \sum_{r \in R} t_r \, r \mid t_r \in T_{\phi} \right\} \] is a set of representatives for the quotient \( A_{\psi}/\mathfrak{m}_{\psi} \) which contains zero, because by definition \( R \subseteq A_{\psi}^{\times} \) was a set of elements whose reduction modulo \( \mathfrak{m}_{\psi} \) gave us a basis for the extension of fields \( A_{\phi}/\mathfrak{m}_{\phi} \subseteq A_{\psi}/\mathfrak{m}_{\psi} \).
To conclude we only need to observe that \( \Pi^{e(\psi \mid \phi)} = u \pi \) for some \( u \in A_{\phi}^{\times} \) because \( \phi(\pi) \) and \( \psi(\Pi) \) generate \( \phi(K^{\times}) \) and \( \psi(L^{\times}) \) respectively. Thus we have that \( \mathfrak{m}_{\psi}^n \) is generated by \( \Pi^n = \pi^i \Pi^j \) with \( 0 \leq j < e(\psi \colon \phi) \) and we can apply Proposition 8 of the ninth lecture to see that every \( \alpha \in A_{\psi} \) can be written as \( \alpha = \sum_{i,j} t_{i,j} \pi^i \Pi^j \) for some \( t_{i,j} \in T_{\psi} \). Thus using the definition of \( T_{\psi} \) we know that every element \( \alpha \in A_{\psi} \) can be written as \[ \alpha = \sum_{r \in R} \sum_{j = 1}^{e(\psi \mid \phi)} \left( \sum_{k = 0}^{+\infty} t_{i,j,k} \pi^k \right) r \Pi^j \] for some \( t_{i,j,k} \in T_{\phi} \). This proves that \[ A_{\psi} = \bigoplus_{r \in R} \bigoplus_{j = 1}^{e(\psi \mid \phi)} A_{\phi} \, r \, \Pi^j \] and thus that the set \( \{ r \, \Pi^j \mid r \in R, \, j \in \{ 1, \dots, e(\psi \mid \phi) \} \, \} \) is a \(K\)-basis for \( L \), which implies that \( f(\psi \mid \phi) e(\psi \mid \phi) = [L \colon K] \) as we wanted to prove. Q.E.D.
Exercise 11 Let \( K \subseteq L \) be an extension of number fields, let \( \mathfrak{P} \subseteq \mathcal{O}_L \) be a prime ideal and let \( \mathfrak{p} := \mathfrak{P} \cap \mathcal{O}_K \). Prove that \( e(\lvert \cdot \rvert_{\mathfrak{P}}, \lvert \cdot \rvert_{\mathfrak{p}}) \) is the maximum of all \( n \in \mathbb{N} \) such that \( \mathfrak{P}^n \mid \mathfrak{p} \mathcal{O}_L \). (Hint: recall what we said in the proof of the previous theorem about the uniformizers...).
Conclusions and references
In this lecture we managed to:- prove that every absolute value which makes a field \( K \) complete admits a unique extension to every finite extension of \( K \);
- prove that every absolute value on a field \( K \) has a finite number of extensions to every finite extension of \( K \);
- define the ramification and inertia index of an extension of valued fields, and prove a fundamental inequality regarding them.
- Section 3 of these notes by Peter Stevenhagen;
- Chapter 2 of the book "Algebraic numbers and algebraic functions" by Paul Moritz Cohn;
- Chapter 17 of the book "Algebraic Number Theory, a Computational Approach" by William Stein.


Comments
Post a Comment