TANT 1 - An introduction to p-adic numbers (and much more)

Hello everyone! These are notes for the first class of the course "Topics in algebra and number theory" held in Block 4 of the academic year 2017/18 at the University of Copenhagen.

This will be a course on p-adic numbers, so in this first hour I tried to give a little motivation about why one should study these objects in relation to some fundamental questions in number theory.

What do we study in number theory?

We started by asking ourselves: what is number theory? This is of course a big question and there is no hope to answer in a short time. However, one may think that number theory is first and foremost the study of the integers $\mathbb{Z}$. This set can be studied as a subset of the real numbers $\mathbb{R}$ by using analytical methods. In this fashion we can ask questions like:

• how many prime numbers are there? In particular, the strong version of the prime number theorem $$\pi(x) = \int_2^x \frac{dt}{\log(t)} + O(\sqrt{x} \log(x))$$ is equivalent to the Riemann hypothesis, one of the most difficult open problems in mathematics. See this paper of Conrey and this paper of Connes for an overview on different approaches to the Riemann Hypothesis;
• how close can prime numbers be? Mayor results in this area are for instance the theorem of Green and Tao, which says that there are arbitrary long arithmetic progressions of prime numbers (see this paper of Conlon, Fox and Zhao for an exposition of the proof) and the twin primes conjecture, which asserts that there are infinitely many couples of primes whose difference is two (see this page for the current records on this conjecture);
• how dense are certain subsets of $\mathbb{Z}$? A big problem along these lines is the conjecture of Goldbach which states that every even integer grater or equal to 4 is a sum of two primes. The best known result in this area is the proof of the fact that every odd integer grater than 5 can be expressed as a sum of three primes (see this book by Harald Helfgott concerning his proof of this result).

Almost all these theorems (and many more) have an heuristic explanation in terms of probabilistic models for the natural numbers (see for instance this blog post by Terence Tao).

We have also another approach to study the integers $\mathbb{Z}$, which is to study them as a ring. Recall in particular that Yoneda's lemma tells us that whenever we have a category $\mathcal{C}$ and we want to study an object $C \in \mathcal{C}$ we may as well study the functor $\operatorname{Hom}(-,C) \colon \mathcal{C}^{\text{op}} \to \mathbf{Sets}$. Applying this to the category $\mathbf{CRings}$ of commutative rings with unity we see that to understand $\mathbb{Z}$ as a ring we need to understand all the possible maps $R \to \mathbb{Z}$, where $R$ is any ring.

This question as it is looks tantalizing, but in fact we shall remember that $\mathbb{Z}$ is also the initial object of the category $\mathbf{CRings}$. Thus for every $R \in \mathbf{CRings}$ we have that $R \cong \mathbb{Z}[\{x_i\}]/(\{f_j\})$ where $\{x_i\}$ is a set of variables and $\{f_j\}$ is a set of polynomials with integer coefficients in a finite number of the $x_i$'s. Now applying the "substitution principle" in commutative algebra (see for example this video by MathProofsable) we see that every map $R \to \mathbb{Z}$ is essentially determined by the integer solutions of a (possibly huge) set of polynomial equations with integer coefficients.

How to (not) solve Diophantine equations

Thus in order to understand $\mathbb{Z}$ as a ring we can, as a first step, try to solve Diophantine equations, i.e. find integer solutions to (systems of) polynomial equations $f(x_1,\dots,x_n) \in \mathbb{Z}[x_1,\dots,x_n]$. This might look simpler at first but is in fact a hugely complicated problem. First of all, the famous theorem of Matiyasevich, Robinson, Davis and Putnam says that it is not possible to find an algorithm which, given any Diophantine equation, would decide whether it has a solution or not (see this survey paper by Martin Davis).

Moreover, finding solutions to Diophantine equations is tremendously difficult also for humans as these two famous examples show:

• the equations $x^n + y^n + z^n = 0$ with $n \in \mathbb{N}_{\geq 3}$ have only solutions $x,y,z \in \mathbb{Z}$ with $x y z = 0$. This is the notorious theorem of Wiles (and many other people) who proved a longstanding conjecture of Fermat (see this survey paper written by Henry Darmon);
• the equations $x^a - y^b - 1 = 0$ with $a, b \in \mathbb{N}_{\geq 2}$ don't have any solution except for the case $a = 2$ and $b = 3$, which has the only solution $(x,y) = (3,2)$. This is the famous conjecture of Catalan, which was proved in 2002 by Preda Mihăilescu (see this survey paper written by Yuri Bilu).

Thus, there is no hope that we will learn in this lecture how to solve all Diophantine equations! Nevertheless we can try to find some methods to solve them in some particular cases. For simplicity we will concentrate on single equations (or, if you prefer, hypersurfaces) of the form $f(x_1,\dots,x_n) = 0$. Thus given a polynomial $f(x_1,\dots,x_n) \in \mathbb{Z}[x_1,\dots,x_n]$ and a ring $R$ we define the set $$X_f(R) := \{\mathbf{x} \in R^n \mid f(\mathbf{x}) = 0 \}$$ and we are interested in particular in the set $X_f(\mathbb{Z})$.

The catch here is that this set is too complicated to be determined with an algorithm (as we have seen) but it is also too simple, i.e. it is just a discrete set with not enough structure to use powerful mathematical tools to study it.

For one thing, $\mathbb{Z}$ is not even a field, so we cannot even take denominators in the solutions of our equation. To put this in a different way, we have that the inclusion $X_f(\mathbb{Z}) \subseteq X_f(\mathbb{Q})$ is usually strict. In order to overcome this difficulty we need to take into consideration the homogenization of the polynomial $f(x_1,\dots,x_n)$. In particular we define $${^h\!f}(x_0,x_1,\dots, x_n) := x_0^d f \left (\frac{x_1}{x_0},\dots, \frac{x_n}{x_0} \right ) \in \mathbb{Z}[x_0,\dots,x_n]$$ where $d$ is the degree of $f$. Observe now that for every ring $R$ we have an action of $R^{\times}$ on the set $X_{{^h\!f}}(R)$ since ${^h\!f}$ is homogeneous. Thus we define $$P_f(R) := \frac{X_{{^h\!f}}(R) \setminus \{\mathbf{0}\}}{R^{\times}}$$ and we observe that in this case $P_f(\mathbb{Z}) = P_f(\mathbb{Q})$. 

Remark This is the wrong definition in general. The right definition would be to take the $R$-points of the scheme $$\mathcal{P}_f := \operatorname{Proj}\left( \frac{\mathbb{Z}[x_0,\dots,x_n]}{( f(x_0,\dots,x_n) )} \right)$$ and the difference between $P_f(R)$ and $\mathcal{P}_f(R)$ lies in the Picard group $\operatorname{Pic}(R)$ of the scheme $\operatorname{Spec}(R)$.

Diving low: reduction modulo primes and local-global principles

So, what do we do now? Well, as a first step we can try to understand whether $P_f(\mathbb{Z}) \neq \emptyset$ or not. In order to do so we can observe that if $P_f(\mathbb{Z}) \neq \emptyset$ then $P_f(\mathbb{Z}/p \mathbb{Z}) \neq \emptyset$ for all prime numbers $p \in \mathbb{Z}$. This gives us a nice necessary condition for $P_f(\mathbb{Z})$ to be non empty which we can easily test with a computer, even by brute force. The problem of course is that we cannot test this for an infinite number of primes, and even if we could do that this wouldn't prove in general that $P_f(\mathbb{Z}) \neq \emptyset$. For example the equation $(x^2 + 1) (x^3 + 3 x + 1) = 0$ has a root in $\mathbb{Z}/p \mathbb{Z}$ for every prime $p$ but does not have a root in $\mathbb{Z}$ (see this question on Math StackExchange). Observe that the previous polynomial is reducible over $\mathbb{Z}$, because for irreducible polynomials in one variable we can indeed check that $P_f(\mathbb{Z}/p \mathbb{Z}) \neq \emptyset$ for all primes $p \in \mathbb{Z}$ to be sure that $P_f(\mathbb{Z}) \neq \emptyset$ (see this question on Math StackExchange).

Is it time to give up already? Maybe not! Indeed, if $P_f(\mathbb{Z}) \neq \emptyset$ then we also have that $P_f(\mathbb{Z}/p^r \mathbb{Z}) \neq \emptyset$ for every prime number $p \in \mathbb{N}$ and every $r \in \mathbb{N}$. Thus we could hope for the converse to this statement to hold!
Actually, this fails to be true (look for example at the equation $x^2 + y^2 + z^2 = 0$) because we are not taking into account all the primes of $\mathbb{Z}$ but only the finite ones. One of the big changes of mentality introduced by the French school (in particular by Weil and Chevalley in the 1940s) is that we should consider also the primes at infinity. We will discover in the following lectures where this name comes from (see here) and how important they are to compactify the spectrum $\operatorname{Spec}(\mathcal{O}_K)$ of the ring of integers of a number field $K$. In particular for our problem of determining whether or not  $P_f(\mathbb{Z}) = P_f(\mathbb{Q}) \neq \emptyset$ this amounts to check also that $P_f(\mathbb{R}) \neq \emptyset$, which is false for $f(x,y,z) = x^2 + y^2 +  z^2$.

Thus we can try to see if it is true that $P_f(\mathbb{Q}) \neq \emptyset$ whenever $P_f(\mathbb{Z}/p^r \mathbb{Z}) \neq \emptyset \neq P_f(\mathbb{R})$. This holds if $f(x)$ is an irreducible polynomial in one variable or if $$f(x_1,\dots,x_n) = \sum_{i=1}^{n}\sum_{j=1}^{n}a_{ij}{x_i}{x_j} \in \mathbb{Z}[x_1,\dots,x_n]$$ is a quadratic form. This is the famous theorem of Hasse and Minkowski (see here for a proof) which could make us hope that this holds in general.

Unfortunately... it is not the case. Already for cubic equations, Selmer showed that $f(x,y,z) = 3 x^3 + 4 y^3 + 5 z^3$ violates this principle, which is now known as the Hasse principle. Nevertheless, it is extremely interesting to try to determine why the Hasse principle fails for certain equations and why it holds for others.

In order to do so, we need to put together all the information that we have on the various rings $\mathbb{Z}/p^r\mathbb{Z}$. First of all we fix the prime $p$ and we let $r \in \mathbb{N}$ vary. If we do so we can define the ring of p-adic integers $$\mathbb{Z}_p := \varprojlim_r \frac{\mathbb{Z}}{p^r \mathbb{Z}}$$ which is an integral domain with fraction field $\mathbb{Q}_p := \operatorname{Frac}({\mathbb{Z}_p})$. Then we take into account all the primes at once, including the prime at infinity, by defining the ring of adeles $$\mathbb{A}_{\mathbb{Q}} := {\prod_p}^{'} (\mathbb{Q}_p \colon \mathbb{Z}_p) \times \mathbb{R}$$ which is a subspace of the "naive" product $\prod_p \mathbb{Q}_p \times \mathbb{R}$ which is too big (i.e. it is not locally compact).

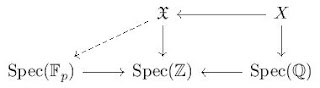
With these new definitions (and in more modern terms) the Hasse principle is the study of the inclusion $X(\mathbb{Q}) \subseteq X(\mathbb{A}_{\mathbb{Q}})$ where $X \to \operatorname{Spec}(\mathbb{Z})$ is a projective scheme of finite type (e.g. $X = \mathcal{P}_f$ for a polynomial $f \in \mathbb{Z}[x_1,\dots,x_n]$). This is related with the Brauer group of the scheme $X$ and is a theme of extremely active research (see these notes of Colliot-Thélène).

Flying up: extensions of $\mathbb{Q}$ and the absolute Galois group

Let's go back to our original question, namely to study the integers $\mathbb{Z}$ as a ring by looking at all the various sets of solutions $X_f(\mathbb{Z})$ for different polynomials $f(x_1,\dots,x_n) \in \mathbb{Z}[x_1,\dots,x_n]$. We saw that one way of approaching this problem is to reduce modulo (powers of) p to get a smaller set to work with. Another possible way of approaching this question could be to get a bigger and richer set to study. One way to do this is to consider finite extensions of $\mathbb{Z}$, e.g. rings of integers $\mathcal{O}_K$ of number fields $K / \mathbb{Q}$. In particular if $K / \mathbb{Q}$ is a finite, Galois extension then $P_f(\mathcal{O}_K) = P_f(K)$ and we have an action of the Galois group $\operatorname{Gal}(K/\mathbb{Q})$ on the set $P_f(K)$. We can thus hope that studying this action could be easier than just studying the smaller set $P_f(\mathbb{Q})$.

If we want to study all the finite extensions $K / \mathbb{Q}$ at once we can consider the inclusion $P_f(\mathbb{Q}) \subseteq P_f(\overline{\mathbb{Q}})$, where $\overline{\mathbb{Q}}$ is an algebraic closure of $\mathbb{Q}$. We have an action of the absolute Galois group $G_{\mathbb{Q}} := \operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})$ over $P_f(\overline{\mathbb{Q}})$ and this action is lossless, i.e. $P_f(\overline{\mathbb{Q}})^{G_{\mathbb{Q}}} = P_f(\mathbb{Q})$. Thus in order to study $P_f(\mathbb{Q})$ we need to study the group $G_{\mathbb{Q}}$ and its representations, i.e. the many possible ways in which it acts on different objects.

This is completely straightforward for irreducible polynomials in one variable $f(x) \in \mathbb{Z}[x]$. Namely if $K_f / \mathbb{Q}$ is the splitting field of $f(x)$ we have that $P_f(\overline{\mathbb{Q}}) = P_f(K_f)$ is a finite set of $d = \deg(f)$ elements which gives us a continuous group homomorphism
$$G_{\mathbb{Q}} \twoheadrightarrow \operatorname{Gal}(K_f/\mathbb{Q}) \hookrightarrow \mathfrak{S}_d \hookrightarrow \operatorname{GL}_d(\mathbb{C})$$ where $\mathfrak{S}_d$ is the symmetric group on $d$ letters and the last map is given by letting $\mathfrak{S}_d$ act on the subscripts of the canonical basis $\mathbf{e}_1,\dots,\mathbf{e}_d$ of $\mathbb{C}^d$. This gives us a tool to study the set $P_f(\mathbb{Q})$ and the extension $K_f / \mathbb{Q}$ by studying the complex representations of the finite group $\operatorname{Gal}(K_f/\mathbb{Q})$.

We can do this also for polynomials with many variables. If we do so we end up with a continuous map of groups $$G_{\mathbb{Q}} \to \operatorname{GL}(\mathbb{C}^{\mathbb{N}})$$ because the set $P_f(\overline{\mathbb{Q}})$ would be countably infinite.
This is not so good to study because we don't have a good theory of infinite dimensional complex representations of groups. To overcome this difficulty we can observe that in the one variable case the representation comes from the geometry of $P_f(\overline{\mathbb{Q}}) = P_f(\mathbb{C})$ which is a finite and discrete topological space.

To see this recall that for every complex manifold $M$ with a continuous action of a group $G$ we get continuous group representations $G \to \operatorname{GL}(H^j_{\text{sing}}(M,\mathbb{C}))$ for every $j = 0, \dots, 2 \dim(M)$.
In particular if $f(x) \in \mathbb{Z}[x]$ is irreducible the only cohomology group of the zero dimensional manifold $P_f(\mathbb{C})$  that it makes sense to consider is $H^0_{\text{sing}}(P_f(\mathbb{C}),\mathbb{C}) \cong \mathbb{C}^d$ where $d = \deg(f)$, and this gives us precisely the representation $G_{\mathbb{Q}} \to \operatorname{GL}_n(\mathbb{C})$ that we defined above.

Thus we can try now to study the higher dimensional complex manifolds $P_f(\mathbb{C})$ for polynomials $f(x_1,\dots,x_n) \in \mathbb{Z}[x_1,\dots,x_n]$. We face two problems:

• $P_f(\overline{\mathbb{Q}}) \neq P_f(\mathbb{C})$ and thus we don't have an action of $G_{\mathbb{Q}}$ on this space but an action of the much bigger group $\operatorname{Aut}_{\mathbb{Q}}(\mathbb{C})$;
• the action of $\operatorname{Aut}_{\mathbb{Q}}(\mathbb{C})$ on $P_f(\mathbb{C})$ is really discontinuous if we consider $P_f(\mathbb{C})$ with the complex topology, and thus doesn't induce an action on cohomology.

For these two reasons (and especially for the second one) we need new cohomology groups to associate to our polynomial $f(x_1,\dots,x_n)$ which would be better related to $P_f(\overline{\mathbb{Q}})$. It was again an incredible result of the French school (and in particular of Grothendieck and Artin) to define cohomology groups $H^j_{\text{ét}}(X_{\overline{\mathbb{Q}}},\overline{\mathbb{Q}}_p)$ using the fields $\mathbb{Q}_p$ for any prime number $p$. Here $X$ is a scheme, a new kind of object which is defined over $\mathbb{Z}$ and encodes both the geometric and the arithmetic properties of the polynomial $f(x_1,\dots,x_n)$. As an example we can take $X = \mathcal{P}_f$ which is the canonical projective scheme associated to a polynomial. In particular there is an operation of base change which allows us to view this object over extensions of $\mathbb{Z}$, e.g. over $\overline{\mathbb{Q}}$ and over $\mathbb{C}$. We will write respectively $X_{\overline{\mathbb{Q}}}$ and $X_{\mathbb{C}}$.

This new cohomology theory is called "étale cohomology" because it is more "calm and rigid" than singular cohomology. In particular these groups are finite dimensional and come with a continuous action of $G_{\mathbb{Q}}$, precisely because they are associated to the base change $X_{\overline{\mathbb{Q}}}$. Moreover, we can recover singular cohomology using étale cohomology! Namely, we get a comparison isomorphism $$H^j_{\text{ét}}(X_{\overline{\mathbb{Q}}},\overline{\mathbb{Q}}_p) \cong H^j_{\text{sing}}(X(\mathbb{C}),\mathbb{C})$$ where $X(\mathbb{C})$ has the complex topology! In this course we will see only an easy ingredient of this proof, namely the fact that we have a (non canonical) isomorphism $\overline{\mathbb{Q}}_p \cong \mathbb{C}$.

Appendix: absolute Galois groups and class field theory

We have seen in this short note how the absolute Galois group $G_{\mathbb{Q}}$ helps us to solve Diophantine equations. In particular every polynomial $f(x_1,\dots,x_n) \in \mathbb{Z}[x_1,\dots,x_n]$ gives us a scheme $\mathcal{P}_f$ which in turn gives us some continuous representations $$G_{\mathbb{Q}} \to \operatorname{GL}\left( H^j_{\text{ét}}((\mathcal{P}_f)_{\overline{\mathbb{Q}}},\overline{\mathbb{Q}}_p) \right) \cong \operatorname{GL}_{h^j}(\mathbb{C})$$ for every prime number $p \in \mathbb{N}$ and every $j = 0, \dots, 2 n$, where $h^j = h^j(\mathcal{P}_f) := \dim(H^j_{\text{ét}}((\mathcal{P}_f)_{\overline{\mathbb{Q}}},\overline{\mathbb{Q}}_p))$.

The group $G_{\mathbb{Q}}$ is the "Holy Grail" of modern number theory. More generally to any field $\kappa$ we can associate an absolute Galois group $G_{\kappa}$ which governs the behavior of the algebraic extensions of $\kappa$. We know really little about absolute Galois groups of fields in general. For example, the inverse Galois problem asks whether every finite group is a quotient of $G_{\mathbb{Q}}$ but we only know this for solvable groups (thanks to the work of Igor Shafarevich), sporadic groups (except, possibly, the Mathieu group $M_{23}$ ) and not so many more. Moreover, we know how to present the group $G_{\kappa}$ only in some special cases:

• by definition $G_{\kappa}$ is trivial if and only if $\kappa$ is algebraically closed;
• when $\kappa = \mathbb{R}$ then $G_{\kappa} \cong \mathbb{Z}/2 \mathbb{Z}$. These two first cases are almost the only cases (up to isomorphism) when $G_{\kappa}$ is finite (see this note by Keith Conrad);
• when $\kappa$ is finite then $G_{\kappa} \cong \varprojlim \mathbb{Z}/n{Z}$ because for every $n \in \mathbb{N}$ any finite field $\kappa$ has a finite Galois extension of degree $n \in \mathbb{N}$, and this extension is unique up to isomorphism (see this note by Miller);
• when $\kappa \supseteq \mathbb{Q}_p$ is a finite extension with $p \neq 2$ then we have an explicit presentation of $G_{\kappa}$ with $[\kappa \colon \mathbb{Q}_p ] + 3$ generators (see Theorem 7.5.14 of the book "Cohomology of number fields" by Neukirch, Schmidt and Wingberg).
• when $\kappa =  \mathfrak{K}(T)$ is a purely transcendental one dimensional extension of an algebraically closed field $\mathfrak{K}$ then $G_{\kappa}$ is isomorphic to the free group on the set of elements of $\mathfrak{K}$. See this paper of Haran and Jarden for a short proof using algebraic methods.

However, giving a presentation of a group is not the only way we have to determine its isomophism class. A deep theorem of Tannaka roughly says that if we have a compact topological group (like $G_{\kappa}$ ) then its isomorphism class is determined by its finite dimensional linear representations over a field (for example, over $\mathbb{C}$). Thus we are back to the problem of studying the representations of $G_{\kappa}$ which were introduced in the previous section as a tool to understand Diophantine equations!

If we want to do this then the first representations that we should study are characters, i.e. (continuous) group homomorphisms $G_{\kappa} \to \mathbb{C}^{\times}$. These maps factor through the abelian part $G_{\kappa}^{\text{ab}}$ of the group $G_{\kappa}$, i.e. the quotient of $G_{\kappa}$ by the subgroup generated by commutators. Describing $G_{\kappa}^{\text{ab}}$ is the subject of class field theory, which gives us a complete answer when $\kappa$ is a number field. In particular, as we will see, we can define a ring of adeles $\mathbb{A}_{\kappa}$ also for general number fields. We have an inclusion $\kappa \subseteq \mathbb{A}_{\kappa}$ and if we define $C_{\kappa} := \mathbb{A}_{\kappa}^{\times} / \kappa^{\times}$ then Artin defined a map $C_{\kappa} \to G_{\kappa}^{\text{ab}}$ which is almost an isomorphism (see this note of Poonen for the correct statement).

If $\kappa = \mathbb{Q}$ this amounts to a theorem of Kronecker and Weber which tells us that every abelian extension of $\mathbb{Q}$ is contained in a cyclotomic extension $\mathbb{Q}(\zeta_n)$ for some $n \in \mathbb{N}$. Modern proofs of this theorem and all the proofs of class field theory use extensively the theory of finite extensions of the p-adic numbers $\mathbb{Q}_p$. Understanding the character theory of $G_{\mathbb{Q}}$ is thus yet another reason to study p-adic fields.

Conclusions and an important attribution

I hope to have convinced you that the p-adic numbers $\mathbb{Q}_p$ are a fundamental tool to study the integers $\mathbb{Z}$ as a ring, which is perhaps the most fundamental question in number theory. They help us to package all the information that we get reducing modulo $p^r$ for various $r \in \mathbb{N}$, they help us to study the representations of the absolute Galois group $G_{\mathbb{Q}}$ (in particular, they are a fundamental tool in class field theory) and they are a crucial ingredient in the definition of étale cohomology, which gives us a big new source of representations of $G_{\mathbb{Q}}$.

Observe finally that p-adic numbers are very similar to the real numbers, which one uses to study "statistical properties" of $\mathbb{Z}$. Recall that $\mathbb{R}$ can be constructed by "filling in the holes" of $\mathbb{Q}$. The key fact here is that this holes are relative to the canonical absolute value $\lvert \cdot \rvert \colon \mathbb{Q} \to \mathbb{R}_{\geq 0}$. As we will see, there are many more absolute values on $\mathbb{Q}$, and there is one of them canonically associated to any prime number $p \in \mathbb{N}$. The result of "filling in the holes" which are relative to this new absolute value is the field $\mathbb{Q}_p$ of p-adic numbers! In particular, we have an inclusion $\mathbb{Z} \subseteq \mathbb{Q}_p$ which allows us to study new "analytic" properties of $\mathbb{Z}$ which are relative to the prime $p$.

Please keep in mind that this class was based on a blog post by Alexander Youcis which is similar to this one. Here you get a little more on analytic number theory and local-global principles, but I didn't have time to treat Legendre's theorem on quadratic forms in detail.